Guía nº 1 de ejercicios resueltos de movimiento armónico simple
Resolver los siguientes ejercicios
� Ver resolución de los ejercicios al pie de la página
Problema nº 1
La ecuación general del movimiento armónico simple es:
X = A·cos [(ω·t) + θ₀]
Puede escribirse en la forma equivalente:
X = B·sen (ω·t) + C·cos (ω·t)
Determínense las expresiones de las amplitudes de B y C en función de la amplitud A y del ángulo de fase inicial θ₀
• Respuesta: B = -A·sen θ₀; C = A·cos θ₀
Problema nº 2
Un cuerpo de 0,25 kg de masa está sometido a una fuerza elástica restauradora, con constante de recuperación k = 25 N/m.
a) Dibújense la gráfica de la energía potencial elástica U en función del desplazamiento x en un intervalo de x comprendido entre -0,3 m y + 0,3 m. Tómense 1 cm = 1 J en el eje vertical y 1 cm = 0,05 m en el eje horizontal.
b) ¿Cuál es la amplitud de la oscilación?
c) ¿Cuál es la energía potencial cuando el valor de desplazamiento es la mitad que el de la amplitud?
d) ¿Para que valor del desplazamiento son iguales la energía cinética y potencial?
e) ¿Cuál es la rapidez del cuerpo en el punto medio de su trayectoria?
f) El período T1.
g) La frecuencia f₁ y
h) La frecuencia angular ω.
i) ¿Cuál es el ángulo de fase inicial θ₀ si la amplitud A = 15 cm, el desplazamiento inicial x₀ = 7,5 cm y la velocidad inicial Vo es negativa?
• Respuesta: b) A = 0,12 m;
c) Eₚ = 4 J;
d) x = ± 0,219 m;
e) v = ±1,26 m/s;
f) T = 0,628 s;
g) f = 1,59 Hz;
h) ω = 10 rad/s;
i) θ₀ = 1,047 rad
Problema nº 3
Un cuerpo está vibrando con movimiento armónico simple de 15 cm de amplitud y 4 Hz de frecuencia, calcúlense:
a) Los valores máximos de la aceleración y de la velocidad.
b) La aceleración y la velocidad cuando el desplazamiento es 9 cm.
c) El tiempo necesario para desplazarse desde la posición de equilibrio a un punto situado a 12 cm de la misma.
• Respuesta:
a) aₘₐₓ = 93,75 m/s² y Vₘₐₓ = 3,76 m/s;
b) a = -56,84 m/s² y V = ± 3,02 m/s;
c) t = 0,025 s
Problema nº 4
Un cuerpo de 10 g de masa se mueve con movimiento armónico simple de 24 cm de amplitud y 4 s de período: El desplazamiento es + 24 cm para t = 0. Calcúlense:
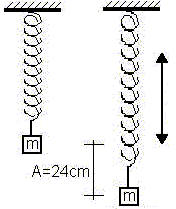
a) La posición del cuerpo cuando t = 0,5 s.
b) La magnitud y dirección de la fuerza que actúa sobre el cuerpo cuando t = 0,5 s.
c) El tiempo mínimo necesario para que el cuerpo se mueva desde la posición inicial al punto en que x = -12 cm, y
d) La velocidad de dicho cuerpo cuando x = -12 cm.
• Respuesta:
a) x = 16,97 cm;
b) F = 418,71 g·cm⁻¹;
c) Δt = 1,33 s;
d) V = -18,67 cm·s⁻¹
Problema nº 5
El movimiento del pistón del motor de un automóvil es aproximadamente armónico simple.
a) Si la carrera de un pistón (dos veces la amplitud) es 10 cm y el motor gira a 3.600 RPM
b) Si el pistón tiene una masa de 0,5 kg, ¿qué fuerza resultante ha de ejercerse sobre él en ese punto?
c) ¿Cuál es la velocidad del pistón, en kilómetros por hora, en el punto medio de su carrera?
• Respuesta:
a) aₘₐₓ = 7.106 m·s²;
b) F = 3.553 N;
c) Vₘₐₓ = 18,85 m/s
Problema nº 6
Un cuerpo de 2 kg de masa está suspendido de un resorte de masa despreciable, y se produce un alargamiento de 20 cm.
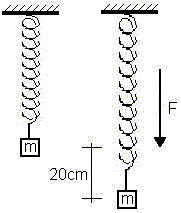
a) ¿Cuál es la constante de recuperación del resorte?
b) ¿Cuál es el período de oscilación del cuerpo si se tira hacia abajo y se abandona así mismo?
c) ¿Cuál sería el período de un cuerpo de 4 kg de masa pendiente del mismo resorte?
• Respuesta:
a) k = 98 N/m;
b) T = 0,89 s;
c) T = 1,26 s
Problema nº 7
La escala de una balanza de resorte que registra de 0 a 180 N tiene 9 cm de longitud. Se observa que un cuerpo suspendido de la balanza oscila verticalmente a 1,5 Hz. ¿Cuál es la masa del cuerpo? Despréciese la masa del resorte.
• Respuesta: m = 22,53 kg
Autor: Jefferson Martínez Jara. Ecuador.