Inferencia estadística-hipótesis (primera parte)
¿Qué es una Hipótesis?
Hipótesis: Es un suposición acerca del valor de un parámetro de una población con el propósito de discutir su validez.
Ejemplo de hipótesis acerca de un parámetro de una población son:
- El sueldo promedio de un profesional asciende a $2,625
- El veinte por ciento de los consumidores utiliza aceite de oliva
¿Qué es una prueba de hipótesis?
Prueba de hipótesis: es un procedimiento, basado en la evidencia de la muestra y en la teoría de las probabilidades, usado para determinar si la hipótesis es una afirmación razonable y debería no ser rechazada o si no es razonable debería ser rechazada.
Prueba de Hipótesis
| Paso 1: Establecer la hipótesis nula y la alternativa | ||||
| ↓ | ||||
| Paso 2: Seleccionar el nivel de significación | ||||
| ↓ | ||||
| Paso 3: Identificar el estadístico de prueba | ||||
| ↓ | ||||
| Paso 4: Formular una regla de decisión | ||||
| ↓ | ||||
| Paso 5: Tomar una muestra, llegar a una decisión | ||||
| ↓ | ↓ | |||
| No realizar la hipótesis | Rechazar la nula y aceptar la alternativa | |||
Definiciones
Hipótesis nula H0: Una afirmación acerca del valor de un parámetro de la población
Hipótesis Alternativa H1: Una afirmación que es aceptada si la muestra provee la evidencia de que la hipótesis nula es falsa
Nivel de significación: La probabilidad de rechazar la hipótesis nula cuando en realidad es verdadera
Error tipo I: Rechazar la nula cuando en realida es verdadera
Error tipo II: Aceptar la hipótesis nula cuando en realidad es falsa
Estadístico de prueba: Es un valor, determinado a partir de la información de la muestra, usado para decidir si rechazar o no la hipótesis nula
Valor crítico: El punto que divide la región entre el lugar en el que la hipótesis nula es rechazada y y la región donde la hipótesis nula es no rechazada
Hipótesis nula unilateral a derecha
Distribución de muestreo para la estadística z
Una cola - nivel de significación 0,05
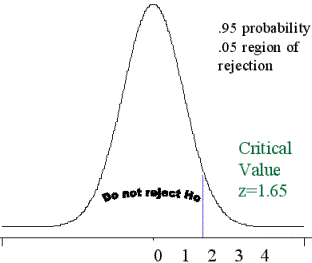
Hipótesis nula bilateral
Distribución de muestreo para la estadística z
A dos colas - nivel de significación 0,05
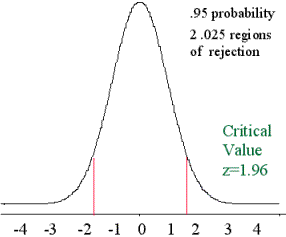
Prueba de hipótesis para la media de una población, muestras grandes, desviación estándar, población conocida
Cuando se plantean hipótesis par la media de la población, a partir de muestras grandes y la desviación estándar poblacional es conocida, el estadísitco de prueba está dado por:
z = (X - μ)/(σ/√n)
Autor: Olga Susana Filippini. Argentina.
Editor: Ricardo Santiago Netto (Administrador de Fisicanet)
- ‹ Anterior
- |
- Siguiente ›
¿Qué es la prueba de chi cuadrado? ¿Qué es la distribución t de Student?