Guía nº 6 de ejercicios de derivadas de funciones trigonométricas inversas en una variable. Problemas con resultado
Resolver los siguientes ejercicios
Problema nº 1
Derivar aplicando funciones trigonométricas inversas.
a) f(x) = arc tg x + arc tg 1/x
• Respuesta: f'(x) = 1
b) f(x) = arc sen 3·x
| Respuesta: f'(x) = | 3 |
| √1 - 9·x² |
c) f(x) = arc sen (cos x)
• Respuesta: f'(x) = -1
| d) f(x) = arc tg | m - x |
| 1 + m·x |
| Respuesta: f'(x) = - | 1 |
| 1 + x² |
e) f(x) = arc sen x + arc sen √1 - x²
• Respuesta: f'(x) = 0
| f) f(x) = arc cos | 1 - x² |
| 1 + x² |
| Respuesta: f'(x) = | 2 |
| 1 + x² |
Problema nº 2
Derivar las siguientes funciones.
a) f(x) = 3·ln² (sen³ eˣ)
• Respuesta: f'(x) = 18·eˣ·ln (sen³ eˣ)·cotg eˣ
b) f(x) = ln √sen √1 - x²
| Respuesta: f'(x) = - | x·cotg √1 - x² |
| 2·√1 - x² |
c) f(x) = ˣ√ln x
| Respuesta: f'(x) = | ˣ√ln x | ·[ | 1 | - ln (ln x)] |
| x² | ln x |
d) f(x) = 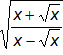
| Respuesta: f'(x) = | √x |
| √x² - x·(x - x²) |
e) f(x) = 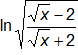
| Respuesta: f'(x) = | 1 |
| (x - 4)·√x |
f) f(x) = ![]()
• Respuesta: f'(x) = ½
• Fuente:
"Apunte nº 448 de análisis matemático y métodos numéricos I". UTN - FRA. 1984.
Autor: Ricardo Santiago Netto. Argentina