Teorema del límite central
Distribución de la media de un muestreo
Sea X₁, X₂, …, Xₙ una muestra aleatoria de una distribución con valor medio μ y desviación estándar σ. Entonces:
1. E(X) = μx = μ
2. V(X) = σx² = σ²/n y σx = σ/√n
Además, con T₀ = X₁ + X₂ + … + Xₙ (la muestra total), E(T₀) = n·μ, V(T₀) = n·σ², y σ·T₀ = √n·σ.
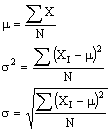
N: número de muestras.
n: número de muestras en el subconjunto extraído del conjunto madre de N muestras.
μx = μₓ
σx² = σ²/n
σx = σ/√n
A medida que aumentan las muestras, la variabilidad disminuye.
Sea X₁, X₂, …, Xₙ una muestra aleatoria de una distribución normal con valor medio μ y desviación estándar σ. Entonces, para cualquier n, X está normalmente distribuida (con media μ y desviación estándar σ/√n), como es T₀ (con media n·μ desviación estándar √n·σ).
Teorema del límite central
Teorema:
Sea X₁, X₂, …, Xₙ una muestra aleatoria de una distribución con media μ y varianza σ². Entonces, si n es suficientemente grande, X tiene aproximadamente una distribución normal con μx = μ y σx² = σ²/n, y T₀ tiene también aproximadamente una distribución normal con μT0 = n·μ, σ²T0 = n·σ². Cuanto más grande sea el valor de n, mejor será la aproximación.
El Teorema del Límite Central garantiza una distribución normal cuando n es suficientemente grande
Si n > 30, se puede usar el TLC.
Si la distribución madre es normal, la distribución de la media muestral también es normal, independientemente del tamaño.
x ≈ N(μₓ; σₓ) ⇒ x ≈ N(μx; σx)
Ejemplo 1:
Si se sabe que la dureza Rockwell de pernos de cierto tipo tiene un valor medio de 50 y desviación estándar de 1,5.
a) Si la distribución es normal, ¿cuál es la probabilidad de que la dureza muestral media para una muestra aleatoria de 9 pernos sea por lo menos 52?
b) ¿Cuál es la probabilidad (aproximada) de que la dureza muestral media para una muestra aleatoria de 40 pernos sea al menos 52?
x = 50
σ = 1,5
x ≈ N(50; 1,5)
a)
n = 9
x = 52
x ≈ N(50; 1,5·√9)
| z = | x - μ |
| σ | |
| √n |
La probabilidad de que la media muestral sea superior a 52 es:
| P(x ≥ 52) = P | x - μ | ≥ | 52 - 50 | ||
| σ | 1,5 | ||||
| √n | √9 |
P(z ≥ 4) = 0
Con el valor de z obtenido de tablas:
| P(x₁ ≤ x ≤ x₂) = P | z₁ ≤ | x - μ | ≤ z₂ | ||
| σ | |||||
| √n |
P(z₁ ≤ z ≤ z₂) = φ(z)
Tener en cuenta que los valores para:
φ(z) = P(z ≤ z₁)
b)
n = 40
Con el valor de z obtenido de tablas:
| P(x ≥ 52) = P | x - μ | ≥ | 52 - 50 | ||
| σ | 1,5 | ||||
| √n | √40 |
P(z ≥ 8,4327) = 0
Bibliografía:
"Probabilidad y estadísticas para ingeniería y ciencias". Jay L. Devore. 1.998.
Autor: Ricardo Santiago Netto. Argentina
¿Qué es la probabilidad? Ejemplos.