Distribuciones discretas y continuas
Binomial y Normal
La Distribución Binomial
Llamaremos experimento dicotómico a un experimento aleatorio cuyos resultados posibles son sólo dos, o nos interesa considerarlos como dos. Por ejemplo:
1) Lanzar una moneda y observar si sale cara o cruz
2) Sacar una carta de una baraja y observar si es una figura o no lo es
3) Elegir una ficha de un dominó y observar si el total de sus puntos es un número par o impar
En este tipo de experiencias a uno de los dos resultados posibles se le suele llamar "éxito" y a su contrario "fracaso". A la probabilidad del suceso llamado éxito se la suele representar por p y a la de su contrario por q. Se verifica, claro está, que p + q = 1 (¿Por qué?). En los ejemplos anteriores podríamos considerar:
1) éxito = "cara", fracaso = "cruz" y, si la moneda no está trucada, p = q = ½
2) éxito = "figura", fracaso = "no figura" y, en una baraja española, p = 12/40 y q = 28/40
3) éxito = "suma par", fracaso = "suma impar" ¿Cuánto valdrían p y q?
Un experimento binomial consiste en repetir una cierta cantidad de veces, y siempre en las mismas condiciones, un experimento dicotómico. Llamaremos "tirada" a cada una de las veces que repetimos el experimento dicotómico. Por ejemplo, son experimento binomiales:
1) Lanzar una misma moneda repetidas veces y observar el número de caras (éxitos) obtenidas
2) Sacar, con reemplazamiento, varias cartas de una misma baraja y observar el número de figuras (éxitos) obtenidas
3) Extraer, con reemplazamiento, varias fichas de un dominó y observar la cantidad de veces que obtenemos una en la que el número total de puntos que aparece es par
Vamos a representar por B(n, p) a una binomial con n tiradas y probabilidad de éxito igual a p.
Puede interesar conocer cual es la probabilidad que de las n pruebas, salgan exactamente x₀ casos favorables a A; o bien calcular la probabilidad que los casos A sean entre x1 y x2, ambos menores que n. Conceptualmente puede decirse que x es una variable aleatoria discreta que toma valores entre 0 (puede no aparecer nunca el suceso) y n (puede aparecer siempre). Es decir que el campo de definición de la variable es: 0 ≤ x ≤ n.
Bajo estas condiciones Bernoulli desarrolló la distribución de probabilidad denominada Binomial, cuya expresión matemática, P(x), está dada por:
P(x) = Cn,x·pˣ·qⁿ ⁻ ˣ
Donde:
x es la variable aleatoria que varía entre 0 y n.
n y p son los datos o parámetros (*) de la distribución binomial.
| Cn,x = | n! |
| n!·(n - x)! |
(Número combinatorio)
Ejemplo de Binomial
De los pinos integrantes de un extenso bosque, un 20 % se encuentra afectado por un hongo parásito. Si se seleccionan al azar 4 pinos, calcular la probabilidad que los afectados por el hongo sean:
a) Exactamente 2
b) Más de uno
Respuesta:
Análisis de las características del problema:
Se realizan 4 observaciones al azar (n = 4 es un dato)
Ante cada observación, los pinos pueden estar A = afectado (por el hongo); = no afectado. Es decir dos resultados posibles en cada prueba.
No se tienen elementos para decir que la probabilidad de que cada pino observado varíe de uno a otro, es decir: p = 0,2 probabilidad de que cada uno de los pinos esté afectado. Será entonces: q = 0,8 probabilidad de pino no afectado.
Las preguntas planteadas se refieren a la cantidad de pinos que resultarán estar afectados (x = variable).
Se dan exactamente las condiciones exigidas para utilizar la Distribución Binomial, y para calcular la probabilidades pedidas, es posible aplicar su función.
a) P(x = 2) = C4,2·0,2²·0,8(4 - 2) = 6·0,04·0,64 = 0,1536
b) P(x > 1) = ∑ C4, x·0,2ˣ·0,84 - x
Sumatoria desde x = 2 hasta 4.
P(x > 1) = 0,1536 + 4·0,008·0,8 + 1·0,0016·1 = 0,1536 + 0,0256 + 0,0016 = 0,1808
También se podría haber calculado como: 1 - P(x < 2).
La Distribución Normal
A lo largo de la historia, matemáticos como De Moivre, Gauss o Galton se sorprendieron por la frecuencia con la que aparece la llamada curva Normal o de Gauss en estudios estadísticos tan aparentemente distintos como la distribución de alturas de un grupo de personas, la resistencia de un tipo determinado de piezas, el número total de caras que obtenemos al lanzar reiteradamente una moneda, y muchos otros.
La curva normal, como cualquier otra curva de probabilidad, verifica que:
- El área total que limita con el eje de abscisas es igual a 1
- La probabilidad de la variable X tome valores entre a y b coincide con el área limitada por la curva, el eje OX y las rectas x = a y x = b
- La probabilidad de que X tome un valor concreto es igual a 0. ¿Por qué?
- No existe una única curva normal; su gráfica, como vas a observar en la siguiente escena, depende de su media, y de su desviación típica
Normal
Distribuciones de probabilidad normales
La distribución de probabilidad normal (D.P.N.) se considera como la distribución de probabilidad más importante. Hay una cantidad ilimitada de variables aleatorias continuas que tienen una distribución normal o aproximadamente normal. La D.P.N. tiene una variable aleatoria contínua y usa dos funciones: una para determinar las ordenadas (valores de y) de la gráfica que representa la distribución, y otra para determinar probabilidades. La siguiente fórmula expresa la ordenada que corresponde a cada abscisa y de denomina función de distribución de probabilidad normal:
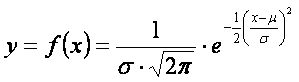
- Para toda x real
- Cuando se traza una gráfica de tales puntos, aparece la curva normal (en forma de campana) como se muestra en el siguiente gráfico:
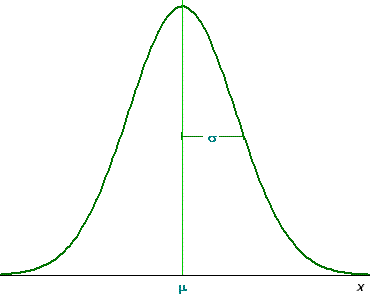
La probabilidad asociada con el intervalo a ≤ x ≤ b está dada por:
| P(a ≤ x ≤ b) = ∫ | a | f(x)·dx |
| b |
La Distribución Normal Estandard
- Hay un número ilimitado de distribuciones de probabilidad normal, aunque afortunadamente todas están relacionadas con una distribución, la distribución normal estandard
- Propiedades de la distribución normal standard
- El área total bajo la curva normal es igual a 1
- La distribución tiene forma de campana y es simétrica; se extiende en ambas direcciones y el eje X es su asíntota
- Tiene media igual a 0 y desviación standard igual a 1
- La media divide el área en dos mitades
- Casi toda el área está entre z = -3 y z = +3
Ejemplo: En una granja modelo de la Provincia de Entre Ríos, en un momento determinado de su desarrollo, los cerdos que producen tienen en cuanto a su peso, una distribución normal con un promedio de 75 kg y un desvío estándar de 6 kg.
Es decir: x ~ N (75, 6) a variable normal estándar será: z = (x - μ)/σ = (x - 75)/6
Donde: z ~ N (0,1)
Con esa información calcular:
P(μ - k·σ < x < μ + k·σ) = P(- k·σ < x - μ < k·σ) = P(- k < (x - μ)/σ < k)
Solución
Dándole valores a k se tiene:
Para k = 1
P(|z| < 1) = P(-1 < z < 1) = F(1) - F(-1) = 0,84134 - 0,15866 = 0,68268
El 68 % de los cerdos tendrán pesos comprendidos entre un desvío estándar en más y en menos de la media (es decir entre 69 y 81 kg) (μ ± σ)
Para k = 2
P(|z| < 2) = P(-2 < z < 2) = F(2) - F(-2) = 0,97725 - 0,02275 = 0,9545
El 95 % de los cerdos tendrán pesos comprendidos entre dos desvíos estándar en más y en menos de la media (es decir entre 63 y 87 kg) (μ ± 2·σ)
Para k = 3
P(|z| < 3) = P(-3 < z < 3) = F(3) - F(-3) = 0,99865 - 0,00135 = 0,9973
Casi el 100 % (99,73 %) de los cerdos tendrán pesos entre tres desvíos estándar en más y en menos de la media (es decir 57 y 93 kg) (μ ± 3·σ)
b)
P(x > 72) = P(z > (x - 75)/6 = -0,50) = 1 - F(-0,50) = 1 - 0,19146 = 0,80854
El 81 % de los cerdos tendrán pesos superiores a 72 kg.
c)
P(69 < x < 87) = P(-1 < z < 2) = F(2) - F(-1) = 0,97725 - 0,15866 = 0,81859
El 82 % de los cerdos tendrán pesos comprendidos entre 69 y 87 kg.
d)
De 20 cerdos elegidos aleatoriamente, ¿cuántos se esperan que pesen más de 81 kg? = 20.
P(x > 81) = 20·P (z > 1) = 20·[1 - F(1)] = 20·(1 - 0,84134) = 20·0,15866 = 3,1732 cerdos
Se espera que tres (o cuatro) cerdos tengan pesos superiores a 81 kg.
e)
¿Cuál es el peso que es superado por el 10 % de los cerdos? Con las tablas que se dispone para este Curso, se tienen algunos valores:
P(x > x₀) = ~ 0,10 ⇒ P(z > z₀) = ~ 0,10 ⇒ z₀ = 1,28;
O bien
P(z ≤ z₀) = ~ 1 - 0,10 ⇒ F (z₀) = ~ 0,90 no disponible en las tablas.
Si z = (x - μ)/σ ⇒ x = z·σ + μ; y para x₀ será:
x₀ = 1,28·6 + 75 = 82,68 kg.
El peso de los cerdos que es superado por el 10 % de ellos es 82,68 kg.
f)
Determinar el valor de peso que supera al 5 % de los cerdos:
P(x < x₀) = P(z < z₀) = 0,05; de donde surge que z₀ es un valor negativo y simétrico a:
P(z > z₀') = 0,05; ⇒ z₀' = 1,645 y será:
z₀ = -1,645 ⇒ x₀ = -1,645·6 + 75 = 65,03 kg.
El peso superado por el 5 % de los cerdos es 65 kg.
Autor: Olga Susana Filippini. Argentina.
Editor: Ricardo Santiago Netto (Administrador de Fisicanet).