Análisis de datos categóricos
En el análisis de datos, especialmente del área biológica (Cs. Naturales, Medicina, Farmacología, etc.) a menudo nos encontramos con mediciones de respuestas que son de naturaleza categórica. Éstas respuestas reflejan información de categorías más que mediciones en escala de intervalos o razón.
Extenderemos los principios básicos de la prueba de hipótesis a situaciones que implican variables categóricas.
Trataremos información que se obtiene del recuento del número de casos que se presentan al estudiar caracteristicas cualitativas
Para el desarrollo de los contenidos correspondientes a esta presentación se ha considerado un hilo conductor según se presenta en el mapa conceptual.
La distribución χ² que hemos visto en los capítulos sobre Estimación de Parámetros y de Pruebas de hipótesis con relación a variancias muestrales, tiene un gran campo de aplicación en el análisis de variables de naturaleza categórica,
Introducción
Si consideramos la situación más sencilla de esta unidad donde cada observación de una muestra se clasifica como pertenecientes a un número finito de categorías:
Ejemplo nº 1
Se observaron 80 nacimientos de un cruzamiento de cerdos de los cuales 42 fueron rojizos, 12 negros y 26 blancos. Las leyes de la herencia implican que estas tres categorías presentan un modelo genético 9:3:4, es decir que deben tener probabilidades 9/16; 3/16 y 4/16 de aparecer en cada cruzamiento. ¿Son los datos consistentes con el modelo teórico propuesto?
Ejemplo nº 2
En la frontera fitosanitaria de la Patagonia se revisaron cargamentos de frutas de distinta procedencia para evaluar la posibilidad de introducción de mosca de las frutas (Ceratitis capitata), una plaga importante de los frutales, en áreas no infestadas. La información de cargamentos con presencia de la plaga se resume en la siguiente tabla:
| Presencia de la plaga | Región de procedencia del cargamento | ||
|---|---|---|---|
| Cuyo | NOA | NEA | |
| Con mosca Sin mosca | 22 67 | 32 5 | 33 10 |
¿Existe alguna dependencia entre la región de procedencia y la presencia de la plaga?
Ejemplo nº 3
Una medicación nueva para tratar cierta enfermedad de vacunos se comparó con la medicación de mayor uso. Para esto se tomó al azar un grupo de 300 animales que padecían la enfermedad; a la mitad de éstos, tomados al azar, se los trató con la nueva medicación y a los otros 150, con la medicación tradicional. Luego de un tiempo se analizaron nuevamente los animales con el siguiente resultado:
| Estado de los animales luego del tratamiento | ||||
|---|---|---|---|---|
| Empeoró | Sin efecto | Mejoró | Totales | |
| Nuevo Tradicional | 16 20 | 30 42 | 104 88 | 150 150 |
| Totales | 36 | 72 | 192 | 300 |
¿Considera que estos medicamentos se comportan de manera similar?
Distribución χ²-cuadrado
Para resolver estos problemas utilizaremos la distribución χ²-cuadrado.
La aplicaremos básicamente:
| χ²-cuadrado | Bondad de Ajuste | Pruebas con probabilidades de cada categoría completamente especificada Bondad de ajuste a una variable discreta Bondad de ajuste a una variable contínua |
| Tablas de contingencia | Pruebas de Homogeneidad Pruebas de Independencia |
Propiedades χ²-cuadrado
Antes de dar una descripción más detallada de estas pruebas repasemos algunas propiedades de esta distribución:
- No toma valores negativos
- Tiene una distribución diferente para cada número de grados de libertad
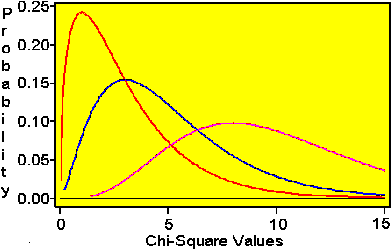
Pruebas de Bondad del Ajuste
(Inferencias acerca del Experimento Multinomial)
- Se desea contrastar una distribución de frecuencias observada en una muestra con una distribución de frecuencias teórica
- Verificar si responde a un determinado modelo o situación preconcebida
- Es una generalización del experimento binomial
- Para aplicar la prueba se necesita una tabla donde se encuentren registradas las frecuencias observadas y las frecuencias teóricas o esperadas según el modelo. El estadístico que se utiliza en estas pruebas es el siguiente:
| χᵥ² = | k ∑ i = 1 | (oᵢ - eᵢ)² |
| eᵢ |
Donde k es el número de categorías y oᵢ y eᵢ son las frecuencia observada y esperada en la i-ésima categoría, respectivamente.
Características de la multinomial
- Consta de n ensayos independientes e idénticos
- El resultado de cada ensayo cae en una de las k categorías posibles (medidas en escala nominal) de la única variable, donde k > 2
- Hay una probabilidad asociada a cada categoria, la cual es constante de un ensayo a otro
- Las categorias son exhaustivas y excluyentes, por lo cual la suma de sus probabilidades es 1
- Se obtienen frecuencias observadas para cada categoría, siendo su suma igual a n
- El número esperado de intentos que resulten en la categoría i es E(Nᵢ) = n·πᵢ, donde πᵢ es la probabilidad de que cualquier observación en particular pertenezca a la categoría i
Prueba de hipotesis para el experimento multinomial
| Hipotesis nula | H₀: π₁, π₂, …, πₖ poseen valores especificados (iguales o no) |
| Hipotesis alternativa | Hₐ: alguna probabilidad de las celdas. Difiere de los valores especificados en H₀ |
| Estadístico de prueba | 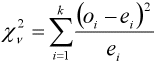 donde o y e representan las frecuencias observadas y esperadas para cada celda |
| Región de rechazo | Esta determinada por la distribución χ², con un determinado α y k - 1 grados de libertad |
| Supuesto | Las frecuencias esperadas no pueden ser en ningún caso inferiores a 5 |
Prueba de hipotesis para el experimento multinomial
- Bajo la hipótesis nula los nᵢ deben estar razonablemente cerca de n·πᵢ
- Cuando los valores de πᵢ difieran marcadamente de lo especificado en la hipótesis nula, los valores observados diferirán de los esperados
- El procedimiento de prueba implica medir las discrepancias entre nᵢ y n·πᵢ, rechazando la hipótesis nula cuando la discrepancia sea suficientemente grande
- Hay solo k - 1 valores de celda determinadas libremente y, por lo tanto, k - 1 grados de libertad
- Dado que grandes discrepancias entre valores observados y esperados conducen a gran valor de ji-cuadrado el rechazo de H₀ es apropiado cuando χ² ≥ χ²α, k - 1 (unilateral a la derecha)
Veamos un ejemplo utilizado en genética acerca de los experimentos clásicos conducidos por Mendel resuelto en la guía teórica.
Mendel tenía arvejas con dos tipos de tegumento, rugoso y liso y, según su hipótesis, en cruzamientos realizados entre ciertos tipos de plantas, el esperaba que aparecieran en la descendencia de dichos cruzamientos, arvejas de tegumento liso y rugoso en la proporción 3:1, es decir, 3 semillas de tegumento liso por cada semilla de tegumento rugoso.
Supongamos que en un experimento en el cual se obtiene una descendencia compuesta por 400 semillas, un genetista encuentra 285 semillas de tegumento liso y 125, de tegumento rugoso. ¿Sería razonable, con α = 0,05, pensar que esa proporción observada no está demasiado alejada de la proporción 3:1 dictada por la ley de Mendel?
- Hipótesis. H₀: La proporción es 3:1; H1: La proporción no es 3:1
- Nivel de significación. α = 0,05
- Estadística de la prueba. Que se distribuye compuesto que, para esta prueba k = 2 y, por consiguiente, υ = 2 - 1 = 1
- Regla de decisión. Rechazamos H0 si, y solo si, el valor de χ2 calculado es mayor que 3,84. En caso contrario, se acepta H₀
| Tegumento | oᵢ | eᵢ | oᵢ - eᵢ | (oᵢ - eᵢ)²/eᵢ |
|---|---|---|---|---|
| Liso Rugoso | 285 115 | 400·¾ = 300 400·¼ = 100 | 15 15 | 0,75 2,25 |
| Total | 400 | 400 | - | 3,00 |
Decisión. Puesto que 3,0 < 3,84 no puede rechazarse H₀ con α = 0,05. Los datos de la muestra no constituyen una prueba suficiente como para dudar de que las proporciones verdaderas son 3:1.
Aún cuando hemos desarrollado la prueba χ²-cuadrado para situaciones donde k > 2, también se puede utilizar cuando k = 2.
La hipótesis nula en este caso se puede expresar como H₀: π₁ = π₁₀
Estas hipótesis también se pueden probar utilizando una prueba z de dos colas con estadísticos de prueba.
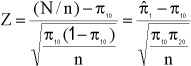
De manera sorprendente, los dos procedimientos de prueba son completamente equivalentes. Esto es porque se puede demostrar que Z² = χ² y (zα/2) = χ²1 α de modo que χ² ≥ χ²α, k - 1 si y sólo si Z ≥ zα/2
Tablas de contingencia con dos criterios de clasificación
En una tabla de contingencia la información está representada por conteos o frecuencias organizadas en i-filas y j-columnas (dos criterios de clasificación). Se presentan dos situaciones:
- Hay i-poblaciones de interés ubicadas cada una en una fila de la tabla y en cada población se describen j-categorías o atributos. Se toma una muestra de cada población y las frecuencias se anotan en la celda de la tabla
- Hay una sola población de interés, y cada individuo es clasificado respecto a dos factores diferentes (i-categorías de un factor j-categorías de otro). Se toma una sola muestra y se anota el número de individuos en cada categoría de ambos factores
Características de las tablas de contingencia
- Consta de n ensayos independientes e identicos
- Hay 2 variables en juego y se representa una tabla de doble entrada
- El resultado de cada ensayo cae en una de las celdas, las cuales resultan de las combinaciones posibles de categorias (medidas en escala nominal) de ambas variables
- Hay una probabilidad asociada a cada celda, la cual es constante de un ensayo a otro
- La probabilidad asociada a cada celda resulta del producto de sus probabilidades marginales
- La suma de las probabilidades asociadas a cada celda es 1
- Se obtienen frecuencias observadas para cada categoria, siendo su suma igual a n
Caso 1: Prueba de homogeneidad
- Ocurre cuando una de las 2 variables es controlada por el investigador, de modo que los totales por fila o por columna están predeterminados
- El analisis es idéntico al de las tablas de contingencia para independencia
- La hipotesis nula que se plantea en este caso consiste en sostener que la distribución de proporciones entre las categorias de la variable no controlada (por fila o por columna) es la misma para cada categoria de la variable controlada
- Otra manera de abordar el mismo problema es preguntarse si las muestras provienen de la misma población
Prueba de hipótesis para prueba de homogeneidad
- Hipótesis. H₀: las i-muestras son extraídas de la misma población. H₁: son extraídas de diferentes poblaciones
- H₀: π1j = π2j = π3j = … = πij
- H₁: H₀ no es verdadera
- Nivel de significación. α = 0,05
- Estadística de la prueba. Que se distribuye aproximadamente como. Aquí υ = (i - 1)·(j - 1)
- Regla de decisión. Rechazamos H₀ si, y solo si, el valor de χ² calculado es mayor que χ²α,(i - 1)·(j - 1). En caso contrario, se acepta H₀
| χᵥ² = | k ∑ i = 1 | (oᵢ - eᵢ)² |
| eᵢ |
El esperado es estimado en cada celda.
| êij = | nᵢ·nj |
| nij |
Ejemplo para prueba de homogeneidad
Objetivo: establecer si las preferencias acerca del envase de dulce de leche son similares para hombres y mujeres
| Envase | Lata | Plástico | Carton | Vidrio | Total |
|---|---|---|---|---|---|
| Varones Mujeres | 27 (19,5) 12 (19,5) | 30 (29,5) 29 (29,5) | 19 (22,5) 26 (22,5) | 24 (28,5) 33 (28,5) | 100 100 |
| Total | 39 | 59 | 45 | 57 | 200 |
h₀: las preferencias (%) acerca del envase de dulce de leche no difieren entre hombres y mujeres
hₐ: las preferencias (%) acerca del envase de dulce de leche difieren entre hombres y mujeres
Estadístico χ²*: 8,296 χ² tabla (α = 0,05; gl = 3): 7,81
Valor p: 0,0402
Conclusión: se rechaza h₀: las preferencias acerca del envase de dulce de leche difieren entre hombres y mujeres
Caso 2: Prueba de independencia.
- Este tipo de prueba se aplica cuando existe interés en determinar si dos atributos categóricos presentan algún tipo de asociación entre ellos o, por el contrario, son independientes
- Este tipo de información se suele presentar en tablas de doble entrada
- El estadístico que se utiliza en estas pruebas es el mismo que el empleado en las pruebas de bondad del ajuste y homogeneidad
- Se estudia la relación entre dos factores diferentes de la misma población
- A diferencia de las pruebas de homogeneidad donde en general los totales de filas están fijos por anticipado, en las pruebas de independencia solo el tamaño muestral es fijo. Por lo tanto los totales de filas como de columnas son variables aleatorias
| Hipotesis nula | H₀: πij = πᵢ* πj las variables son independientes |
| Hipotesis alternativa | Hₐ: πij ≠ πᵢ* πj las variables no son independientes |
| Estadístico de prueba | χ² = ∑(O - E)²/E donde O y E representan las frecuencias observadas y esperadas para cada celda |
| Región de rechazo | Esta determinada por la distribución χ², con un determinado α y (i - 1)·(j - 1) grados de libertad (gl) |
Ejemplo para prueba de independencia.
Una muestra de 500 estudiantes ingresantes en una universidad participó en un estudio diseñada con el fin de evaluar el grado de conocimiento en matemáticas. La siguiente tabla muestra los estudiantes clasificados según su formación secundaria (escuelas técnicas, bachiller y otras) y el nivel de conocimiento en matemáticas (bueno = aprobó el examen; deficiente = no aprobó el examen):
| Bueno | Deficiente | |
|---|---|---|
| Técnicas Bachiller Otras | 20 15 25 | 60 150 230 |
¿Confirman estos datos que la aptitud en matemáticas depende de la orientación de los estudios secundarios?
H₀: La aptitud en matemáticas es independiente de la orientación del secundario
H₁: La aptitud en matemáticas es dependiente de la orientación del secundario
Estadístico χ²*: 15,289 χ² tabla (α = 0,05; gl = 2): 5,99
Valor p: 0,00047845
Conclusión: se rechaza h₀: La aptitud en matemáticas es independiente de la orientación del secundario, por lo tanto, las variables son dependientes.
Precauciones en la interpretación de resultados
- Los grados de libertad dependen de la cantidad de categorías de las variables y no del número de casos, de modo que el valor de tabla no se modifica al aumentar el número de casos
- Utilizando muestras grandes, se dice poca cosa al decir que una relación es significativa, ya que es relativamente fácil establecer significación, aún en el caso de que la relación existente sea muy superficial
Autor: Olga Susana Filippini. Argentina.
Editor: Ricardo Santiago Netto (Administrador de Fisicanet).
¿Qué es una prueba de bondad?