Guía n° 4 de ejercicios de casos de factoreo o factorización

Resolver los siguientes ejercicios

Definición:

Factorizar o factorear una expresión algebraica es convertirlo o descomponerlo en un producto de expresiones algebraicas más simples.

Así, se llama factores o divisores de una expresión algebraica a las expresiones algebraicas que multiplicadas entre sí dan como producto la 1^ra expresión.

Ejemplos:

a) 6·x² - 5·x - 6 = (2·x - 3)·(3·x + 2)

b) m⁴ - n⁴ = (m² + n²)·(m + n)·(m - n)

c) a⁵ - x⁵ = (a - x)·(a⁴ + a³·x + a²·x² + a·x³ + x⁴)

d) a⁵ + b⁵ = (a + b)·(a⁴ - a³·b + a²·b² - a·b³ + b⁴)

e) a⁴ - b⁴ = (a + b)·(a³ - a²·b + a·b² - b³)

• 7^mo Caso: Trinomio de la forma a·x² + b·x + c.

Es aquel trinomio cuyo 1^er término tiene un coeficiente distinto de 1.

Ejemplos:

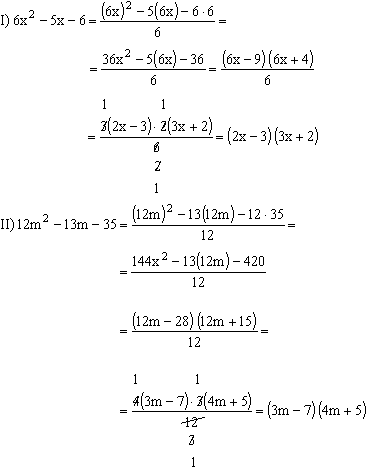
Ejercicios de aplicación

1) 2·x² + 3·x - 2

2) 2·y² + 29·y + 90

3) 2·m² + 11·m + 5

4) 2·a² + a - 3

5) 2·n² + 5·n + 2

6) 2·a² - 7·a + 3

7) 3·x² - 5·x - 2

8) 3·a² + 7·a - 6

9) 3·x² - 7·x - 10

10) 3·y² + 9·y + 6

11) 3·a² - 13·a - 30

12) 4·a² + 15·a + 9

13) 4·m² + m - 33

14) 5·y² - 2·y - 7

15) 5·x² + 13·x - 6

16) 6·n² - 7·n - 3

17) 6·x² + 7·x + 2

18) 6·a² - 5·a - 6

19) 7·y² - 23·y + 6

20) 7·x² - 44·x - 35

21) 8·a² - 14·a - 15

22) 9·n² + 10·n + 1

23) 9·y² - 21·y + 12

24) 9·x² + 37·x + 4

25) 10·a² + 11·a + 3

26) 10·m² - m - 2

27) 10·x² + 7·x - 12

28) 12·m² - 13·m - 35

29) 12·x² - x - 6

30) 12·x² - 7·x - 12

31) 14·m² - 31·m - 10

32) 15·n² + n - 6

33) 15·m² + 16·m - 15

34) 15·a² - 8·a - 12

35) 15·b² - 16·b + 4

36) 18·a² - 13·a - 5

37) 20·x² + 7·x - 6

38) 20·y² + y - 1

39) 20·m² + 44·m - 15

40) 20·n² - 9·n - 20

41) 20·a² - 7·a - 40

42) 21·x² + 11·x - 2

43) 30·m² + 13·m - 10

44) 6·x⁴ + 5·x² - 6

45) 7·y⁴ - 33·y² - 10

46) 8·n⁴ - 2·n² - 15

47) 10·m⁴ - 23·m² - 5

48) 12·a⁴ - 19·a² - 18

49) 14·m⁴ - 45·m² - 14

50) 15·x⁴ - 11·x² - 12

51) 15·a⁴ - 17·a² - 4

52) 2·a⁶ + 5·a³ - 12

53) 5·x⁶ + 4·x³ - 12

54) 7·m⁶ - 33·m³ - 10

55) 2·a² + a·b - 3·b²

56) 4·m² - 20·m·n + 9·n²

57) 4·x² - 11·x·y + 6·y²

58) 5·a² - 2·a·b - 7·b²

59) 6·a² + 13·a·b + 6·b²

60) 6·x² - 11·a·x - 10·a²

61) 6·m² - 13·a·m - 15·a²

62) 6·a² - a·x - 15·x²

63) 9·x² + 6·x·y - 8·y²

64) 15·m² - a·m - 2·a²

65) 18·a² + 17·a·y - 15·y²

66) 20·a² - 27·a·b + 9·b²

67) 21·x² - 29·x·y - 72·y²

68) 30·a² - 13·a·b - 3·b²

69) 30·m² + 17·a·m - 21·a²

70) 4·a⁴ - 10·a²·b + 6·b²

71) 4·x⁴ - 12·x²·y + 5·y²

72) 4·a⁴ - 20·a²·b + 9·b²

73) 6·m⁴ + 13·m²·n + 6·n²

74) 9·x⁴ + 6·x²·y - 8·y²

75) 15·m⁴ - a·m² - 2·a²

76) 12·x² - 19·x·y² - 18·y⁴

• 8^vo Caso: Suma o Diferencia de potencias de igual grado con exponente par o impar.

a)

Suma de potencias de igual grado con exponente par.

No se puede factorear; pues la suma de potencias de igual grado de exponente par nunca es divisible ni por la suma ni por la diferencia de sus bases.

Ejemplos:

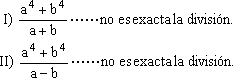
b)

Suma de potencias de igual grado con exponente impar.

En éste caso; la suma de potencias de igual grado de exponente impar únicamente es divisible por la suma de sus bases.

Ejemplos:

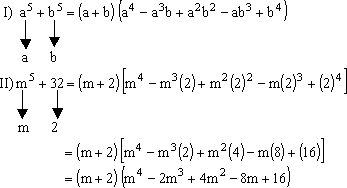
Ejercicios de aplicación

1) a³ + 1

2) x³ + 1

3) y³ + 1

4) a³·b³·x³ + 1

5) a³ + 8

6) m³ + 27

7) x³ + 125

8) n³ + 1.000

9) m³ + 8·a³x³

10) x³ + y³

11) 8·a³ + b³

12) 27·m³ + n³

13) 8·x³ + 27·y³

14) 8·a³ + 125·b³

15) 27·m³ + 8·n³

16) 343 + 8·a³

17) 1 + a³

18) 1 + m³

19) 1 + 216·b³

20) 1 + 343·n³

21) a⁵ + 1

22) a⁵ + 243

23) x⁵ + 32

24) m⁵ + 32

25) b⁵ + 1/32

26) a⁵ + 32·b⁵

27) a⁵ + b⁵·c⁵

28) a⁵ + b⁵

29) a⁵ + x⁵

30) b⁵ + y⁵

31) m⁵ + n⁵

32) x⁵ + m⁵

33) x⁵ + y⁵

34) 32·x⁵ + 1

35) 1 + 243·y⁵

36) a⁷ + 1

37) b⁷ + 1

38) n⁷ + 128

39) y⁷ + 2.187

40) a⁷ + b⁷

41) m⁷ + n⁷

42) x⁷ + y⁷

43) 1 + b⁷

44) 1 + x⁷

45) 1 + 128·a⁷

c)

Diferencia de potencias de igual grado con exponente par.

En éste caso; la diferencia de potencias de igual grado de exponente par es divisible por la suma y por la diferencia de sus bases. También se puede factorear como diferencia de cuadrados (el más usado).

Ejemplos:

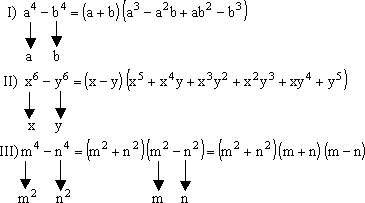
Ejercicios de aplicación

1) a⁴ - 1

2) n⁴ - 81

3) b⁴ - 625

4) a⁴ - b⁴·c⁴

5) x⁴ - y⁴

6) m⁴ - n⁴

7) a⁴·x⁴ - m⁴

8) x⁴ - 16·m⁴·n⁴

9) 16·m⁴ - 81·n⁴

10) 81·x⁴ - 16·y⁴

11) 625 - n⁴

12) a⁶ - 1

13) m⁶ - 64

14) x⁶ - 729

15) b⁶ - 729

16) x⁶ - a⁶·y⁶

17) a⁶ - b⁶

18) x⁶ - y⁶

19) 729·a⁶ - 1

20) 1 - a⁶·b⁶

21) 64 - x⁶

22) a⁸ - b⁸

23) m⁸ - n⁸

24) x⁸ - y⁸

25) 1 - a⁸

26) 256 - y⁸

d)

Diferencia de potencias de igual grado con exponente impar.

En éste caso; la diferencia de potencias de igual grado de exponente impar únicamente es divisible por la diferencia de sus bases.

Ejemplos:

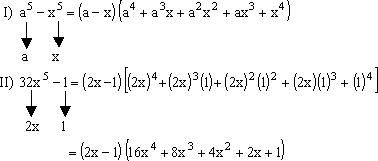
Ejercicios de aplicación

1) a³ - 1

2) y³ - 1

3) a³ - 8

4) x³ - 27

5) b³ - 64

6) x³ - 216

7) a³ - 125

8) b³ - 8·a³

9) a³ - b³

10) m³ - n³

11) x³ - y³

12) m³ - 8·n³

13) 8·x³ - 1

14) 8·m³ - 1

15) 27·a³ - 1

16) 1.000·y³ - 1

17) 8·x³ - 125

18) 64·a³ - 729

19) 27·a³ - b³

20) 27·m³ - n³

21) 8·m³ - 27·n³

22) 1 - b³

23) 1 - m³

24) 1 - 8·x³

25) 1 - 27·a³·b³

26) 1 - 216·m³

27) a⁵ - 1

28) m⁵ - 32·n⁵

29) a⁵ - b⁵

30) a⁵ - x⁵

31) a⁵ - 243·b⁵

32) 32·m⁵ - 1

33) 1 - x⁵

34) 1 - 32·y⁵

35) 32 - m⁵

36) 243 - 32·b⁵

37) a⁷ - 1

38) b⁷ - 1

39) x⁷ - 1

40) n⁷ - 128

41) y⁷ - 2.187

42) a⁷ - b⁷

43) m⁷ - n⁷

44) x⁷ - y⁷

45) m⁷ - a⁷·x⁷

46) a⁷ - 128·b⁷

47) 1 - n⁷

48) 1 - y⁷

49) 1 - 128·a⁷

Autor: Hugo David Giménez Ayala

Paraguay.

Editor: Ricardo Santiago Netto (Administrador de Fisicanet)

Ver condiciones para uso de los contenidos de fisicanet.com.ar

• 🔍
• ✉ f t

Factorizar expresiones algebraicas. Diferencia de potencias de igual grado.