Guía nº 8 de problemas de funciones

Resolver los siguientes ejercicios

Problema nº 1

Graficar las siguientes funciones:

a) f(x) = (x + 2)²

b) f(x) = -(x - 3)²

c)

d)

e)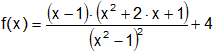

f)

g)

h) f(x) = -x·(x + 4)²

i) f(x) = x·(x - 2)·(x + 3)

j)

Problema nº 2

Indicar en cada uno de los ejercicios anteriores el dominio y la imagen de cada función.

Problema nº 3

Representar en el plano real las siguientes regiones:

a) A = {(x; y) ∈ ℜ²/x ≥ 4}

b) B = {(x; y) ∈ ℜ²/-1 ≤ x ≤ 4}

c) C = {(x; y) ∈ ℜ²/2 ≤ x ≤ 3 ∧ -1 ≤ y ≤ 1}

d) D = {(x; y) ∈ ℜ²/|x| ≤ 3}

e) E = {(x; y) ∈ ℜ²/|x| ≤ 2 ∧ |y| ≥ 3}

f) F = {(x; y) ∈ ℜ²/x - y + 1 = 0}

g) G = {(x; y) ∈ ℜ²/|x + y| = 1}

¿Cuál de las relaciones dadas son funciones?

Problema nº 4

Representar gráficamente:

a) y = |x|

b) y = |x| - 3

c) y = 1 - |x|

d) f(x) = |x| + x + 2

e) f(x) = |4 - 3·x|

f) f(x) = |x + 2| + |x| + |x - 2|

g)

Problema nº 5

Dado:

a)

P(x) = a - (2·a - 4)·x² + 3·a·x

Calcular "a" para que la función sea afín.

b)

Si Q(x) = (2·a + b)·x² - (1 - 2·b)·x + ½·(b - a)

Calcular "a" y "b" para que Q(x) sea una función constante.

Autor: Ricardo Santiago Netto. Argentina