Guía nº 13 de problemas de funciones logarítmicas

Resolver los siguientes ejercicios

Problema nº 1

Sabiendo el log 2 = 0,301 y el log 3 = 0,477, calcular:

a)

b) log 5

c) log 0,27

d) log 0,0128

Problema nº 2

Hallar el campo de definición (o dominio) de las siguientes funciones:

a) f(x) = log (x - 5)

b) g(x) = log₆ (x² - 3·x - 4)

c)

d)

Problema nº 3

Resolver las siguientes ecuaciones:

a) 2·log (log x) = log (7 - 2·log x) - log 5

b) log_½ (1/16) + 2·log₃ (x - 3)·log₃ (x + 2) = log₃² (x - 3) + log₃² (x + 2) ⟶ ℜ: x = 29/8

c)

d)

e) log₂² x - 9·log₈ x = 4

f) 4ˣ + 6ˣ - 2·9ˣ = 0

g)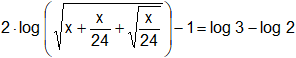

h) log² 100·x + log² 10·x + log x = 14

i) x + log (1 + 2ˣ) = x·log 5 + log 6

j) log⁻¹ x = 2 + log⁻¹ x

k) 3ˣ ⁺ ¹ + 2·3^{2 - x} - 29 = 0

l)

m)

n) x²˙ˣ - (x² + x)·xˣ + x³ = 0

o) log (x³ - 6·x² + 11·x - 5) = 0

p) log³ x + log⁹ x = log⁸¹ x + 5/2

q)

r)

s) log_½ 1/16 + 2·log₃ (x - 3)·log₃ (x + 2) = log₃²(x - 3)·log₃²(x + 3)

Problema nº 4

Calcular:

a)

b)

Problema nº 5

Para qué valores de n ∈ ℜ se verifica:

a)

b)

Problema nº 5

Resolver las siguientes desigualdades:

a) log_½ (x² - 3/2) ≥ 1

b) 0 < log₂ (2·x - 1) ≤ 1

c) log_½ (x + 2) + log_½ (x - 3) > 2

Problema nº 6

Demostrar que:

(logₐ b)·(log_b a) = 1

Problema nº 7

Determinar la base de los siguientes logaritmos:

a) logₓ 2 = ⅓

b) logₓ 5 = ⅓

c) logₓ 5 = -⅓

d) logₓ 0,25 = 2

e) logₓ 16 = -2

Autor: Ricardo Santiago Netto. Argentina