Guía nº 14 de problemas de funciones logarítmicas
Resolver los siguientes ejercicios
Problema nº 1
Resolver las siguientes sistemas aplicando logaritmos:
a)
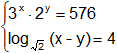
b)
![]()
c)
![]()
d)
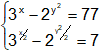
e)
![]()
f)
![]()
g)
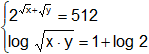
h)
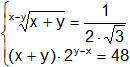
i)
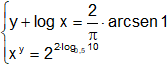
j)
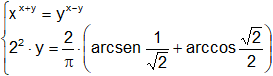
k)
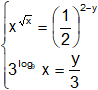
Problema nº 2
Resolver aplicando logaritmos:
a)
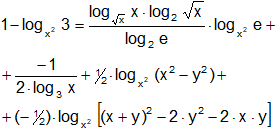
b)
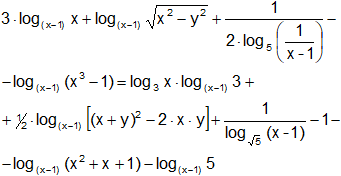
c)
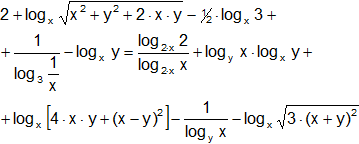
Problema nº 3
Sabiendo que a² + b² = 7·a·b, demostrar que:
log [⅓·|a + b|] = ½·(log |a| + log |b|)
Problema nº 4
Resolver:
log (x³) = (log x)³
Problema nº 5
Calcular:
2x² = 6
Problema nº 6
¿Qué relación existe entre logₐ b y logb a?
Problema nº 7
Calcular:
a) x = (log 2 - log 0,2 + log 0,02)⁻colog 100, tomar log 2 = 0,301
b) x = (colog 0,01 - log 0,01)colog 1.000
Autor: Ricardo Santiago Netto. Argentina