Guía nº 15 de problemas de funciones
Resolver los siguientes ejercicios
Problema nº 1
Determinar el dominio de las siguientes funciones empleando intervalos cuando sea posible:
a) f = {(x, y): ∈ ℜ²/y = 1/x}
b) f(x) = (2·x - 1)/(x + 3)
c) f(x) = x/(x² + 1)
d) f(x) = √x - x²
e) f(x) = (4·x - 1)/(x² - 1)
f) f(x) = √1 - x
g) f(x) = √(x + 1)/(x - 3)
Problema nº 2
Representar gráficamente las siguientes funciones cuadráticas, llevar previamente a la forma cónica y = a·(x - m)² + k:
a) y = x² - 2·x + 5
b) y = x² - 6·x + 14
c) f(x) = -2·x² + 4·x + 3
Problema nº 3
Graficar las siguientes funciones:
a)
| f(x) = | x si x < 1 1 si 1 ≤ x ≤ 2 2·x - 3 si 2 < x < 3 3 si x ≥ 3 |
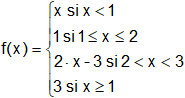
b)
| y = | |x| si x < -1 x² si -1 ≤ x ≤ 1 |x| si x > 1 |
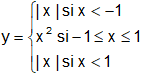
Problema nº 4
Indicar si las siguientes funciones son inyectivas o subyectivas, justificar:
a) f(x) = 2·x - 1
b) f(x) = x² + 4
c) f(x) = x³
Problema nº 5
Indicar cuáles de las siguientes funciones son biyectivas, para las mismas, hallar f⁻¹ y hacer el gráfico de ambas sobre un mismo sistema de ejes:
a) f(x) = 3·x - 2
b) f(x) = + √x - 1
c) f(x) = 2·x² - 1
Problema nº 6
Dadas las funciones f:ℜ ⟶ ℜ / f(x) = x + 3 ∧ g:ℜ ⟶ ℜ / g(x) = x², se pide:
a) Calcular g[f(0)]; g[f(-2)]
b) Determinar [g o f](x) = g[f(x)]
Problema nº 7
Dadas las funciones:
f:ℜ ⟶ ℜ/f(x) = (x + 1)/x ∧ g:ℜ ⟶ ℜ/g(x) = 2·x + 1
Calcular:
[g o f](x) = f[g(x)] y [g o f](x) = g[f(x)]
Problema nº 8
Dadas las funciones:
f:ℜ ⟶ ℜ / f(x) = x² - 2·x ∧ g:ℜ ⟶ ℜ / g(x) = x² + 1
Calcular [g o f](-2) + [f o g](0)
Problema nº 9
Dada f(x) = a·x + b; p y q números reales y distintos, calcular f(p), f(q) y demostrar que:
[f(p) - f(q)]/(p - q) = a
Problema nº 10
Dada f(x) = -4·x + 3, sin efectuar los cálculos, cuál es el valor de:
[f(1.000) - f(100)] /900
Problema nº 11
Hallar la ecuación de la recta que pasa por:
a) (1, 1) ∧ (-2, 2)
b) (-3, 1) ∧ (2, 2)
Autor: Ricardo Santiago Netto. Argentina