Funciones de varias variables

Idea intuitiva: Hasta el momento hemos trabajado con función de una sola variable, es decir, que van de ℜ a ℜ. Ahora vamos a trabajar con funciones escalares, que reciben un vector de ℜⁿ y devuelven un valor de ℜ, y con funciones vectoriales que reciben un vector de ℜⁿ y devuelven uno de ℜᵐ. La dificultad de estas funciones reside en que no tienen representación gráfica posible, a excepción de las funciones de ℜ² en ℜ, que se pueden representar como superficies tridimensionales. Además, los cálculos de límites se complican mucho llegando a ser imposibles. Por ello nos ocuparemos casi siempre de las más sencillas de este tipo de funciones, aunque toda la teoría se referirá a funciones de n variables.

Conceptos básicos

Definición:

Sea f:ℜⁿ ⟶ ℜ una aplicación que a cada x ∈ ℜⁿ le asigna f(x) ∈ ℜ. Entonces f:ℜⁿ ⟶ ℜ es una función escalar de varias variables.

x = (x₁, … xₙ) ∈ ℜⁿ

f(x) = f(x₁, … xₙ) = t ∈ ℜ

Notación: En el caso de que n = 2, haremos:

x₁ = x, x₂ = y

Y en el caso de que n = 3

x₁ = x, x₂ = y, x₃ = z

Definición:

Sea f:ℜⁿ ⟶ ℜ. Llamamos dominio de la función al conjunto de puntos de ℜⁿ en el que está definida f:ℜⁿ ⟶ ℜ

Ejemplo nº 1

f(x, y) = [ln (x² + y² - 25)]/(x + y²)

Dom(f) = {(x, y) ∈ ℜ²/ x² + y² > 25, x ≠ -y²}

Observación:

Sea f:ℜ² ⟶ ℜ. Llamamos gráfica de f al conjunto {(x, y, z) ∈ ℜ³ / z = f(x, y) ⊂ ℜ³}. A dicha gráfica la llamaremos superficie:

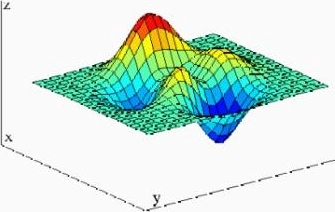
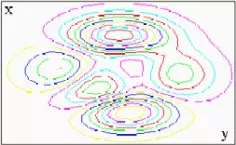
Ejemplo nº 2

Llamamos curvas de nivel a los puntos de la forma {(x, y) ∈ ℜ²/ f(x, y) = constante}. Son los puntos obtenidos al intersectar la superficie generada por f con un plano z = constante, y proyectarla en el plano.

Observación:

Sea f:ℜ³ ⟶ ℜ. Llamamos superficies de nivel de f a los conjuntos de la forma conjunto {(x, y, z) ∈ ℜ³ / f(x, y, z) = constante}.

Definición:

Sea f:ℜⁿ ⟶ ℜᵐ una aplicación que a cada x ∈ ℜⁿ le asigna un vector f(x) = Y ∈ ℜᵐ. Entonces f:ℜⁿ ⟶ ℜᵐ es una función vectorial de varias variables.

x = (x₁, … xₙ) ∈ ℜⁿ

f(x) = [f₁(x), f₂(x), …, fₘ(x)] ∈ ℜᵐ, fᵢ: ℜⁿ ⟶ ℜ

Y a las f₁:ℜⁿ ⟶ ℜ se las llama funciones coordenadas.

Ejemplo nº 3

f(x, y) = [(x + y)/(x - y), sen (x + y), cos (x·y)] f:ℜ² ⟶ ℜ³

Definición:

Sea f:ℜⁿ ⟶ ℜᵐ. Llamamos Dominio de la función a la intersección de los dominios de las funciones coordenadas de f.

Autor: José Luis Martínez-Avila. España.

Editor: Ricardo Santiago Netto (Administrador de Fisicanet).

Definición de función escalar de varias variables. Superficies y curvas de nivel.