Problema nº 12 de funciones de varias variables, derivadas direccionales

Enunciado del ejercicio nº 12

Calcular las derivadas direccionales de la siguiente función, en los puntos indicados y según las direcciones indicadas:

f(x, y) = log y/log x

Desarrollo

Datos:

Dᵤf(X) = ∇f(X)·u

Para:

u = (u₁, u₂)

u₁ = cos ·u

u₂ = cos ·u

o

Para:

Máxima velocidad de crecimiento de una función f(X) en un punto dado X₀ es:

||∇f(X₀)||

Dirección de máxima velocidad de crecimiento de una función f(X) en un punto dado X₀ es:

∇f(X₀) ⇔ (si: ∇f(X₀) ≠ 0)

Solución

El gradiente es:

∇f(x, y) = [(-log y)/(x·log² x), 1/(y·log x)]

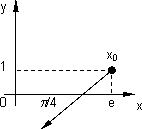
Los datos del gráfico son:

X₀ = (e, 1)

u = (u₁, u₂)

u = (-½·, -½·)

El gradiente calculado en el punto es:

∇f(e, 1) = [(-log 1)/(e·log² e), 1/(1·log e)] = (-0/e·1, 1/1·1) = (0, 1)

Resultado, la derivada direccional es:

Dᵤ(e, 1) = (0, 1)·(-½·, -½·) = -½·

Resolvió: Ricardo Santiago Netto. Argentina

Ejemplo, cómo hallar las derivadas direccionales