Integrales dobles (primera parte)
F:A ⊂ ℜ² ⟶ ℜ S ⊂ A
∬d F(x, y)·dx·dy
Interpretación geométrica en ℜ³: volumen debajo del gráfico de F
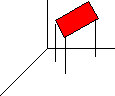
Gráfico de interpretación del volumen bajo la curva
Teorema de Fubini
| ∬ₛ F(x, y)·dx·dy = ∫ | b1 | [∫ | b2 | F(x, y)·dy]·dx = ∫ | b2 | [∫ | b1 | F(x, y)·dy]·dx (*) |
| a1 | a2 | a2 | a1 |
(*) Caso de limites bien definidos
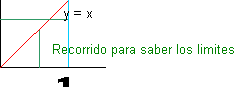
Gráfico del recorrido para determinar los límites
| ∫ | 1 | ∫ | x | dy·dx = ∫ | 1 | ∫ | y | dx·dy |
| 0 | 0 | 0 | 0 |
Propiedades:
1) Dadas F y G continuas en A ⊂ ℜ², y dadas α y β ∈ ℜ:
∬A (α·F + β·G)(x, y)·dx·dy = α·∬A F(x, y)·dx·dy + β·∬A G(x, y)·dx·dy
2) Dadas F y G continuas en A ⊂ ℜ² tales que F(x, y) ≥ G(x, y), ∀ (x, y) ∈ A:
∬A F(x, y)·dx·dy ≥ ∬A G(x, y)·dx·dy
Cálculo de áreas
Área (A) = ∬A dx·dy
Ejemplo:
Calcular el área de A ⊂ ℜ², limitada por las curvas y = eˣ, y = e⁻ˣ, y = e²
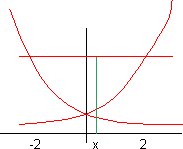
Gráfico de las curvas que limitan el área de integración
| Área = ∫ | 0 | [∫ | e² | dy]·dx + ∫ | 2 | [∫ | e² | dy]·dx |
| -2 | e⁻ˣ | 0 | eˣ |
Cálculo de masas
Masa = ∬A δ(x, y)·dx·dy donde δ(x, y) es la densidad superficial
Centro de masa
X (cm) = ∬A x·δ(x, y)·dx·dy/M
Y (cm) = ∬A y·δ(x, y)·dx·dy/M
Teorema:
∬A F(x, y)·dx·dy = ∬A+ F(G(u, v))·|det DG|·du·dv
Observaciones: det DG ≠ 0 para formar un área.
Editor: Ricardo Santiago Netto (Administrador de Fisicanet).
¿Para qué sirven las integrales dobles? Integrales dobles aplicaciones.