Ejemplo, cómo calcular las coordenadas del baricentro.

Problema n° 12 de integrales

Enunciado del ejercicio n° 12

{(x, y): (x - 2)²/4 + y² ≤ 1, x ≥ 2}

Si:

X_G =	∬_D x·dx·dy
	∬_D dx·dy

Y_G =	∬_D y·dx·dy
	∬_D dx·dy

Cambiando de sistema de coordenadas:

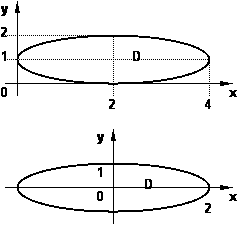
Gráfico del dominio para el cálculo de baricentro

Con el dominio:

{(x, y): (x/2)² + y² ≤ 1, x ≥ 0}

y = 0 es eje de simetría, entonces:

Y_G = 0

Cambiando a coordenadas cilíndricas:

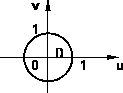
Gráfico del dominio en coordenadas cilíndricas para el cálculo de baricentro

x = 2·u ⇒ u = x/2

y = v

|J| = 2 ⇒ dx·dy = 2·du·dv

Con el dominio:

{(u, v): u² + v² ≤ 1, u ≥ 0}

Si: X_G = I/A

Luego:

I = ∬_D x·dx·dy = ∬_D' 2·u·2·du·dv

I = 4·∬_D' u·du·dv

Por simetría con respecto a y = 0:

I = 8·∬_D" u·du·dv

Con:

{(u, v): u² + v² ≤ 1, u ≥ 0, v ≥ 0}

Cambiando a sistema de coordenadas polares:

u = r·cos θ

v = r·sen θ

|J| = r

du·dv = r·dθ·dr

Para:

0 ≤ r ≤ 1

0 ≤ θ ≤ π/2

I = 8·∬_D" r·(cos θ)·r·dθ·dr

I = 8·∬_D" r²·(cos θ)·dθ·dr

I = 8·∫	π/2	dθ∫	1	r²·cos θ·dr

	0		0

Luego:

I = 8·∫	π/2	(⅓·r³·cos θ)	1	·dθ

	0		0

I = 8·⅓·∫	π/2	(r³·cos θ)	1	·dθ

	0		0

I = 8·⅓·∫	π/2	(1³·cos θ - 0³·cos θ)·dθ

	0

I = 8·⅓·∫	π/2	cos θ·dθ

	0

I = 8·⅓·(sen θ)	π/2

	0

I = (8/3)·[sen (π/2) - sen 0]

I = (8/3)·1

I = 8/3

Para calcular A debemos tener en cuenta el dominio original y en forma práctica se trata de media área de elipse:

A = ∬_D·dx·dy = a·b·π/2 = 1·2·π/2

A = π

Finalmente:

X_G = I/A = (8/3)/π = 8/(3·π)

Resultado, el baricentro es:

G = [8/(3·π), 0]

Autor: Ricardo Santiago Netto (Administrador de Fisicanet)

San Martín. Buenos Aires. Argentina.

Ver condiciones para uso de los contenidos de fisicanet.com.ar

🔍
✉ f t