Problema nº 8 de integrales, coordenadas del baricentro de un sólido
Enunciado del ejercicio nº 8
D = {(x, y, z): x² + y² ≤ 2·z, x² + y² ≤ 1, x² + y² + z² ≤ 9}
Las ecuaciones de las coordenadas son:
| xG = | ∭D x·dx·dy·dz | = | Iₓ |
| ∭D dx·dy·dz | VD | ||
| yG = | ∭Dy·dx·dy·dz | = | Iy |
| ∭D dx·dy·dz | VD | ||
| zG = | ∭D z·dx·dy·dz | = | Iz |
| ∭D dx·dy·dz | VD | ||
Para el dominio:
Por simetría del dominio con respecto al plano y = 0, y por asimetría de la integranda con respecto al plano y = 0, resulta:
Para la simetría del dominio se debe cumplir f(x, y) = f(x, -y)
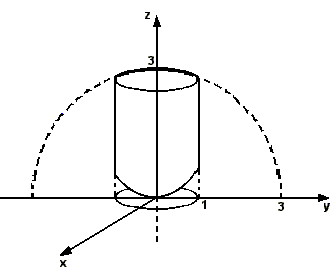
Gráfico del dominio para el cálculo de baricentro del sólido
Para el paraboloide:
f(x, y) = (x² + y²)/2
f(x, -y) = [x² + (-y)²]/2 = (x² + y²)/2
Cumple.
Para el cilindro:
f(x, y) = x² + y²
f(x, -y) = x² + (-y)² = x² + y²
Cumple.
Para la semiesfera:
f(x, y, z) = f(x, -y, z)
f(x, y, z) = x² + y² + z²
f(x, -y, z) = x² + (-y)² + z² = x² + y² + z²
Cumple.
Para la asimetría de la integranda se debe cumplir f(x, -y) = -f(x, y)
Para la coordenada en Y:
f(x, y) = y ⇒ -f(x, y) = -y
f(x, -y) = -y
Cumple.
Por lo tanto YG = 0
Para la coordenada en x ocurre que por simetría del dominio con respecto al plano x = 0, y por asimetría de la integranda con respecto al plano x = 0, resulta:
Para la simetría del dominio se debe cumplir f(x, y) = f(-x, y)
Para el paraboloide:
f(x, y) = (x² + y²)/2
f(-x, y) = [(-x)² + y²]/2 = (x² + y²)/2
Cumple.
Para el cilindro:
f(x, y) = x² + y²
f(-x, y) = (-x)² + y² = x² + y²
Cumple.
Para la semiesfera:
f(x, y, z) = f(-x, y, z)
f(x, y, z) = x² + y² + z²
f(-x, y, z) = (-x)² + y² + z² = x² + y² + z²
Cumple.
Para la asimetría de la integranda se debe cumplir f(-x, y) = -f(x, y)
Para la coordenada en X:
f(x, y) = x ⇒ -f(x, y) = -x
f(-x, y) = -x
Cumple.
Por lo tanto XG = 0
Para calcular el volumen aplicamos la primera fórmula de reducción para un dominio base Dxy de la función superior menos la función inferior:
VD = ∭D·dx·dy·dz
VD = ∬Dxy [β(x, y) - α(x, y)]·dx·dy
VD = ∬Dxy [√9 - (x² + y²) - ½·(x² + y²)]·dx·dy
Pasando a coordenadas polares:
0 ≤ r ≤ 1
0 ≤ θ ≤ 2·π
|J| = r
VD = ∬D'xy (√9 - r² - ½·r²)·r·dr·dθ
VD = ∬D'xy (r·√9 - r² - ½·r³)·dr·dθ
VD = ∬D'xy r·√9 - r²·dr·dθ - ½·∬D'xy r³·dr·dθ
| VD = ∫ | 2·π | dθ∫ | 1 | r·√9 - r²·dr - ½·∫ | 2·π | dθ∫ | 1 | r³·dr |
| 0 | 0 | 0 | 0 |
Si:
u = 9 - r²
du = -2·r·dr ⇒ -du/2 = r·dr
| VD = -½·∫ | 2·π | dθ∫ | 1 | √u·du - ½·∫ | 2·π | dθ∫ | 1 | r³·dr |
| 0 | 0 | 0 | 0 |
| VD = -½·∫ | 2·π | ⅔·[u3/2] | 1 | ·dθ - ½·∫ | 2·π | ¼·[r⁴] | 1 | ·dθ |
| 0 | 0 | 0 | 0 |
| VD = -½·∫ | 2·π | ⅔·[9 - r²]3/2 | 1 | ·dθ - ½·∫ | 2·π | ¼·(1⁴ - 0⁴)·dθ |
| 0 | 0 | 0 |
| VD = -½·∫ | 2·π | ⅔·[(9 - 1²)3/2 - (9 - 0²)3/2)]·dθ - ½·∫ | 2·π | (¼)·dθ |
| 0 | 0 |
| VD = -½·⅔·∫ | 2·π | (83/2 - 93/2)·dθ - ½·¼·∫ | 2·π | dθ |
| 0 | 0 |
| VD = -⅓·∫ | 2·π | (√2⁹ - √3⁶)·dθ -⅛·∫ | 2·π | dθ |
| 0 | 0 |
VD = -⅓·(2⁴·√2 - 3³)·2·π - ⅛·2·π
VD = -⅔·(16·√2 - 27)·π - ¼·π
VD = [-⅔·(16·√2 - 27) - ¼]·π
VD = (-128·√2 + 216 - 3)·π/12
VD = (-128·√2 + 216 - 3)·π/12
VD = (-128·√2 + 213)·π/12
VD = (213 - 128·√2)·π/12
Iz = ∭D z·dx·dy·dz
| Iz = ∬Dxy dx·dy∫ | β(x, y) | z·dz |
| α(x, y) |
| Iz = ∬Dxy dx·dy∫ | √9 - (x² + y²) | z·dz |
| (x² + y²)/2 |
| Iz = ∬Dxy [½·z²] | √9 - (x² + y²) | ·dx·dy |
| (x² + y²)/2 |
Iz = ½·∬Dxy {[√9 - (x² + y²)]² - [½·(x² + y²)]²}·dx·dy
Iz = ½·∬Dxy [9 - (x² + y²) - ¼·(x² + y²)²]·dx·dy
Cambiando a sistema de coordenadas polares:
| 0 ≤ r ≤ 1 0 ≤ θ ≤ 2·π | ⟶ |J| = r |
Iz = ½·∬D'xy (9 - r² - ¼·r⁴)·r·dr·dθ
Iz = ½·∬D'xy (9·r - r³ - ¼·r⁵)·dr·dθ
| Iz = ½·∫ | 2·π | dθ∫ | 1 | (9·r - r³ - ¼·r⁵)·dr |
| 0 | 0 |
Como las variables son independientes en la integral:
| Iz = ½·2·π·∫ | 1 | (9·r - r³ - ¼·r⁵)·dr |
| 0 |
| Iz = π·∫ | 1 | (9·r - r³ - ¼·r⁵)·dr |
| 0 |
| Iz = π·[9·½·r² - ¼·r⁴ - ¼·⅙·r⁶] | 1 |
| 0 |
Iz = π·[(9/2)·(1² - 0²) - ¼·(1⁴ - 0⁴) - (1/24)·(1⁶ - 0⁶)]
Iz = π·(9/2 - 1/4 - 1/24)
Iz = π·(108 - 6 - 1)/24
Iz = π·101/24
Calculando la coordenada:
| ZG = | Iz |
| VD |
| 101 | ·π | ||
| ZG = | 24 | ||
| 213 - 128·√2 | ·π | ||
| 12 | |||
| ZG = | 101 | · | 1 |
| 2 | 213 - 128·√2 |
| ZG = | 101 |
| 2·(213 - 128·√2) |
Expresando el baricentro como punto:
| G = [0, 0, | 101 | ] |
| 2·(213 - 128·√2) |
Resolvió: Ricardo Santiago Netto. Argentina
Ejemplo, cómo calcular las coordenadas del baricentro de un sólido.