Problema nº 15 de integrales, baricentro de un dominio plano
Enunciado del ejercicio nº 18
r ≤ 2·θ, 0 ≤ θ ≤ π
Si:
| XG = | ∬D x·dx·dy |
| ∬D dx·dy | |
| YG = | ∬D y·dx·dy |
| ∬D dx·dy | |
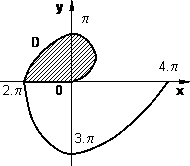
Gráfico del dominio para el cálculo de baricentro
Calculando el área con un cambio de fórmula a coordenadas polares:
| AD = ∬D dx·dy = ½·∫ | β | (r(θ))²·dθ |
| α |
| AD = ½·∫ | π | (2·θ)²·dθ |
| 0 |
| AD = ½·∫ | π | 4·θ²·dθ |
| 0 |
| AD = 2·∫ | π | θ²·dθ |
| 0 |
| AD = 2·⅓·θ³ | π |
| 0 |
AD = ⅔·π³
Para mayor claridad en la resolución:
XG = I₁/AD
YG = I₂/AD
Cambiando a coordenadas polares:
x = r·cos θ
y = r·sen θ
|J| = r·dr·dθ
0 ≤ θ ≤ π
0 ≤ r ≤ 2·θ
Resolviendo:
I₁ = ∬D x·dx·dy
I₁ = ∬D' r²·(cos θ)·dr·dθ
| I₁ = ∫ | π | cos θ·dθ∫ | 2·θ | r²·dr |
| 0 | 0 |
| I₁ = ∫ | π | cos θ·(⅓·r³) | 2·θ | ·dθ |
| 0 | 0 |
| I₁ = ∫ | π | ⅓·cos θ·(2·θ)³·dθ |
| 0 |
| I₁ = ⅓·∫ | π | cos θ·8·θ³·dθ |
| 0 |
| I₁ = ⅓·8·∫ | π | θ³·cos θ·dθ |
| 0 |
| θ³ | + | cos θ |
| 3·θ² | - | sen θ |
| 6·θ | + | -cos θ |
| 6 | - | -sen θ |
| 0 | + | cos θ |
| I₁ = ⅓·8·(θ³·sen θ + 3·θ²·cos θ - 6·θ·sen θ - 6·cos θ) | π |
| 0 |
I₁ = (8/3)·[(π³·sen π + 3·π²·cos π - 6·π·sen π - 6·cos π) - (0³·sen 0 + 3·0²·cos 0 - 6·0·sen 0 - 6·cos 0)]
I₁ = (8/3)·(3·π²·cos π - 6·cos π + 6·cos 0)
I₁ = (8/3)·[3·π²·(-1) - 6·(-1) + 6·1]
I₁ = (8/3)·(-3·π² + 6 + 6)
I₁ = (8/3)·(-3·π² + 12)
I₁ = 8·[-π² + 4)
I₂ = ∬D y·dx·dy = ∬D' r²·(cos θ)·dr·dθ
| I₂ = ∫ | π | sen θ·dθ∫ | 2·θ | r²·dr |
| 0 | 0 |
| I₂ = ∫ | π | sen θ·(⅓·r³) | 2·θ | ·dθ |
| 0 | 0 |
| I₂ = ∫ | π | ⅓·sen θ·(2·θ)³·dθ |
| 0 |
| I₁ = ⅓·∫ | π | sen θ·8·θ³·dθ |
| 0 |
| I₁ = ⅓·8·∫ | π | θ³·sen θ·dθ |
| 0 |
| θ³ | + | sen θ |
| 3·θ² | - | -cos θ |
| 6·θ | + | -sen θ |
| 6 | - | cos θ |
| 0 | + | sen θ |
| I₂ = ⅓·8·(-θ³·cos θ + 3·θ²·sen θ + 6·θ·cos θ - 6·sen θ) | π |
| 0 |
I₂ = (8/3)·(-π³·cos π + 6·π·cos π)
I₂ = (8/3)·[-π³·(-1) + 6·π·(-1)]
I₂ = (8/3)·(π³ - 6·π)
I₂ = (8·π/3)·(π² - 6)
Reemplazando:
| XG = | I₁ |
| AD |
| XG = | 8·(-π² + 4) |
| ⅔·π³ |
| XG = | 3·4·(-π² + 4) |
| π³ |
| XG = | 12·(-π² + 4) |
| π³ |
| YG = | I₂ |
| AD |
| YG = | (8·π/3)·(π² - 6) |
| ⅔·π³ |
| YG = | 4·(π² - 6) |
| π² |
Expresando el punto:
| G = [ | 12·(-π² + 4) | , | 4·(π² - 6) | ] |
| π³ | π² |
Resolvió: Ricardo Santiago Netto. Argentina
Ejemplo, cómo hallar el baricentro de un dominio plano