Problema n° 15 de integrales
Enunciado del ejercicio n° 15
Calcular el baricentro del dominio plano encerrado por la cardioide r = 1 - cos θ.
Como la función integranda es antisimétrica con respecto al eje y, y el dominio es simétrico con respecto al mismo eje, resulta:
yG = 0
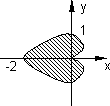
Gráfico del dominio para el cálculo de baricentro
Ahora calculamos el área del dominio directamente en coordenadas polares:
A = ∬D r·dr·dθ
0 ≤ r ≤ 1 - cos θ
0 ≤ θ ≤ 2·π
| A = ∫ | 2·π | dθ∫ | 1 - cosθ | r·dr |
| 0 | 0 |
| A = ∫ | 2·π | (½·r²) | 1 - cosθ | ·dθ |
| 0 | 0 |
| A = ∫ | 2·π | ½·(1 - cos θ)²·dθ |
| 0 |
| A = ½·∫ | 2·π | (1 - 2·cos θ + cos² θ)·dθ |
| 0 |
| A = ½·[θ - 2·sen θ + ½·(θ + sen θ·cos θ)] | 2·π |
| 0 |
A = ½·[2·π - 2·sen 2·π + ½·(2·π + sen 2·π·cos 2·π)] - ½·[0 - 2·sen 0 + ½·(0 + sen 0·cos 0)]
A = ½·[2·π - 2·0 + ½·(2·π + 0·1)] - ½·[-2·0 + ½·(0·1)]
A = ½·(2·π + ½·2·π)
A = ½·(2·π + π)
A = π + ½·π
A = 3·π/2
Luego calculamos el numerador:
A = ∬D x·dx·dy = ∬D' r²·(cos θ)·dr·dθ
0 ≤ r ≤ 1 - cos θ
0 ≤ θ ≤ 2·π
| Ix = ∫ | 2·π | cos θ·dθ∫ | 1 - cos θ | r²·dr |
| 0 | 0 |
| Ix = ∫ | 2·π | cos θ·⅓·(r³) | 1 - cos θ | ·dθ |
| 0 | 0 |
| Ix = ∫ | 2·π | cos θ·⅓·(1 - cos θ)³·dθ |
| 0 |
| Ix = ⅓·∫ | 2·π | cos θ·(1 - 3·cos θ + 3·cos² θ - cos³ θ)·dθ |
| 0 |
| Ix = ⅓·∫ | 2·π | cos θ·dθ - ∫ | 2·π | cos² θ·dθ + ∫ | 2·π | cos³ θ·dθ - ⅓·∫ | 2·π | cos4 θ·dθ |
| 0 | 0 | 0 | 0 |
Reemplazando:
cos² θ = ½·(1 + cos 2·θ)
cos4 θ = ¼·(1 + cos 2·θ)²
cos4 θ = ¼·(1 + 2·cos 2·θ + cos² 2·θ)
| Ix = ⅓·∫ | 2·π | cos θ·dθ - ½·∫ | 2·π | (1 + cos 2·θ)·dθ + ∫ | 2·π | (1 - sen² θ)·cos θ·dθ - (1/12)·∫ | 2·π | (1 + 2·cos 2·θ + cos² 2·θ)·dθ |
| 0 | 0 | 0 | 0 |
| Ix = ⅓·[sen θ] | 2·π | - ½·[½·θ + ½·sen 2·θ] | 2·π | + ∫ | 2·π | (cos θ - cos θ·sen² θ)·dθ - (1/12)·[θ + sen 2·θ + ½·θ + ½·sen θ·cos θ] | 2·π |
| 0 | 0 | 0 | 0 |
| + [sen θ] | 2·π | - [⅓·sen³ θ] | 2·π | - (1/12)·(2·π + sen 2·2·π + ½·2·π + ½·sen 2·π·cos 2·π - sen 0 - ½·sen 0·cos 0) |
| 0 | 0 |
Ix = ⅓·(sen 2·π - sen 0) - ½·(½·2·π + ½·sen 2·π·cos 2·π - ½·sen 0·cos 0) +
Ix = -π + (sen 2·π - sen 0) - (⅓·sen³ 2·π - ⅓·sen³ 0) - (2·π + π)/12
Ix = -π - 3·π/12
Ix = -π - π/4
Ix = -5·π/4
Autor: Ricardo Santiago Netto. Argentina
Ejemplo, cómo hallar el baricentro de un dominio plano