Problema nº 9 de integrales, flujo saliente a través de un cubo
Enunciado del ejercicio nº 15
Calcular el flujo saliente del campo anterior a través del embudo determinado por las superficies:
| S₁: x² + y² = 1 | ⟶ | 0 ≤ z ≤ 1 |
| S₂: x² + y² - z² = 0 | ⟶ | 1 ≤ z ≤ 4 |
Desarrollo
Fórmulas:
∬S F(x) = ∬D F(X(u, v))·(Xᵤ ∧ Xᵥ)·du·dv
Solución
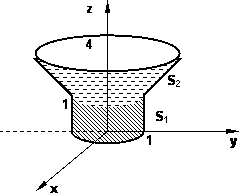
Gráfico del dominio para el cálculo de la superficie
Aplicamos la fórmula para las superficies por separado, luego el flujo total será la suma de ambos flujos.
Parametrizamos la primera superficie:
X(θ, z) = (cos θ, sen θ, z)
| D₁: 0 ≤ z ≤ 1 ⟶ | 0 ≤ θ ≤ 2·π 0 ≤ z ≤ 1 |
Calculamos n:
Xθ = (- sen θ, cos θ, 0)
Xz = (0, 0, 1)
| n = | E₁ | -E₂ | E₃ | = (cos θ, -(-sen θ), 0) = (cos θ, sen θ, 0) |
| - sen θ | cos θ | 0 | ||
| 0 | 0 | 1 |
n = (cos θ, sen θ, 0)
F(X(θ, z)) = (cos θ, sen θ, 2·π - cos θ - sen θ)
El flujo saliente de la primera superficie será:
Flujo₁ = ∬S1 F(x)
Flujo₁ = ∬D1 F(X(θ, z))·n·dθ·dz
Flujo₁ = ∬D1 (cos θ, sen θ, 2·π - cos θ - sen θ)·(cos θ, sen θ, 0)·dθ·dz
Flujo₁ = ∬D1 (cos² θ + sen² θ)·dθ·dz
Flujo₁ = ∬D1 dθ·dz
| Flujo₁ = ∫ | 2·π | dθ∫ | 1 | ·dz |
| 0 | 0 |
| Flujo₁ = 2·π·(z) | 1 |
| 0 |
Flujo₁ = 2·π
Parametrizamos la segunda superficie:
X(θ, z) = (z·cos θ, z·sen θ, z)
| D₂: 1 ≤ z ≤ 4 ⟶ | 0 ≤ θ ≤ 2·π 1 ≤ z ≤ 4 |
Calculamos n:
Xθ = (- z·sen θ, z·cos θ, 0)
Xz = (cos θ, sen θ,1)
| n = Xθ ∧ Xz = | E₁ | -E₂ | E₃ | = [z·cos θ, -(- sen θ), -z·(sen θ)·(sen θ) - z·(cos θ)·(cos θ)] |
| - z·sen θ | z·cos θ | 0 | ||
| cos θ | sen θ | 1 |
n = (z·cos θ, z·sen θ, - z·sen² θ - z·cos² θ)
n = (z·cos θ, z·sen θ, - z·(sen² θ + z·cos² θ)) = (z·cos θ, z·sen θ, - z)
F(X(θ, z)) = (z·cos θ, z·sen θ, 2·z - z·cos θ - z·sen θ)
El flujo saliente de la segunda superficie será:
Flujo₂ = ∬S2 F(x)
Flujo₂ = ∬D2 F(X(θ, z))·n·dθ·dz
Flujo₂ = ∬D2 (z·cos θ, z·sen θ, 2·z - z·cos θ - z·sen θ)·(z·cos θ, z·sen θ, -z)·dθ·dz
Flujo₂ = ∬D2 (z²·cos² θ + z²·sen² θ - z·(2·z - z·cos θ - z·sen θ))·dθ·dz
Flujo₂ = ∬D2 (z²·(cos² θ + sen² θ) - 2·z² + z²·cos θ + z²·sen θ)·dθ·dz
Flujo₂ = ∬D2 (z² - 2·z² + z²·cos θ + z²·sen θ)·dθ·dz
Flujo₂ = ∬D2 z²·(- 1 + cos θ + sen θ)·dθ·dz
| Flujo₂ = ∫ | 2·π | dθ∫ | 4 | z²·(-1 + cos θ + sen θ)·dz |
| 0 | 1 |
| Flujo₂ = ∫ | 2·π | (⅓·z³) | 4 | ·(-1 + cos θ + sen θ)·dθ |
| 0 | 1 |
| Flujo₂ = ∫ | 2·π | (⅓·4³ - ⅓·1³)·(-1 + cos θ + sen θ)·dθ |
| 0 |
| Flujo₂ = ∫ | 2·π | (⅓·64 - ⅓)·(-1 + cos θ + sen θ)·dθ |
| 0 |
| Flujo₂ = ∫ | 2·π | ⅓·63·(-1 + cos θ + sen θ)·dθ |
| 0 |
| Flujo₂ = 21·∫ | 2·π | (-1 + cos θ + sen θ)·dθ |
| 0 |
| Flujo₂ = 21·[-θ + sen θ + (-cos θ)] | 2·π |
| 0 |
Flujo₂ = 21·(-2·π + (sen 2·π - sen 0) - (-0 + cos 2·π - cos 0))
Flujo₂ = 21·(-2·π - (1 - 1))
Flujo₂ = -42·π
El flujo total es:
Flujo = Flujo₁ + Flujo₂
Resultado, el flujo saliente del campo es:
Flujo = 2·π - 42·π
Flujo = -40·π
Resolvió: Ricardo Santiago Netto. Argentina
Ejemplo, cómo calcular el flujo saliente a través de una superficie