Problema n° 9 de integrales

Enunciado del ejercicio n° 9

Calcular el flujo saliente del campo (z, x, y) a través del cubo, 0 ≤ x ≤ 1, 0 ≤ y ≤ 1, 0 ≤ z ≤ 1.

∬_S F(x) = ∬_D F(X(u, v))·(X_u ∧ X_v)·du·dv

Dividimos la superficie según las caras:

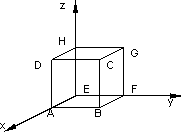
Gráfico del dominio para el cálculo de la superficie

S₁: ABFE ⟶ X(x, y) = (x, y, 0)

S₂: DCGH ⟶ X(x, y) = (x, y, 1)

S₃: ABCD ⟶ X(y, z) = (1, y, z)

S₄: EFGH ⟶ X(y, z) = (0, y, z)

S₅: AEHD ⟶ X(x, z) = (x, 0, z)

S₆: BFGC ⟶ X(x, z) = (x, 1, z)

Las derivadas y los vectores normales son:

X'_x = (1, 0, 0), X'_y = (0, 1, 0) ⇒ N₁ = (0, 0, 1)

X'_x = (1, 0, 0), X'_y = (0, 1, 0) ⇒ N₂ = (0, 0, 1)

X'_y = (0, 1, 0), X'_z = (0, 0, 1) ⇒ N₃ = (1, 0, 0)

X'_y = (0, 1, 0), X'_z = (0, 0, 1) ⇒ N₄ = (1, 0, 0)

X'_x = (1, 0, 0), X'_z = (0, 0, 1) ⇒ N₅ = (0, 1, 0)

X'_x = (1, 0, 0), X'_z = (0, 0, 1) ⇒ N₆ = (0, 1, 0)

Luego:

F₁(X(x, y)) = (0, x, y)

F₂(X(x, y)) = (1, x, y)

F₃(X(y, z)) = (z, 1, y)

F₄(X(y, z)) = (z, 0, y)

F₅(X(x, z)) = (z, x, 0)

F₆(X(x, z)) = (z, x, 1)

Las integrales son:

∬_S1 F(x)·ds = ∬_D1 (0, x, y)·(0, 0, 1)·dx·dy = ∬_D1 y·dx·dy

∬_S2 F(x)·ds = ∬_D2 (1, x, y)·(0, 0, 1)·dx·dy = ∬_D2 y·dx·dy

∬_S3 F(x)·ds = ∬_D3 (z, 1, y)·(1, 0, 0)·dy·dz = ∬_D3 z·dy·dz

∬_S4 F(x)·ds = ∬_D4 (1, 0, y)·(1, 0, 0)·dy·dz = ∬_D4 z·dy·dz

∬_S5 F(x)·ds = ∬_D5 (z, x, 0)·(0, 1, 0)·dx·dz = ∬_D5 x·dx·dz

∬_S6 F(x)·ds = ∬_D6 (z, x, 1)·(0, 1, 0)·dx·dz = ∬_D6 x·dx·dz

Aplicando los signos según la orientación y sumando:

∬_S F·ds = -∬_D1 y·dx·dy + ∬_D2 y·dx·dy + ∬_D3 z·dy·dz - ∬_D4 z·dy·dz - ∬_D5 x·dx·dz + ∬_D6 x·dx·dz

∬_S F·ds = 0

Autor: Ricardo Santiago Netto. Argentina

Ejemplo, cómo calcular el flujo saliente a través de un cubo