Propiedades de los números complejos I
1. Números concretos
Un número complejo Z es un par ordenado de números reales (a, b), a y b ∈ ℜ
a = 1° componente o componente real
b = 2° componente o componente imaginaria.
Z₁ = (a, 0) es un número real
Z₂ = (0, b) es un número imaginario
Z₃ = (a, b) es un número complejo
2. Unidad imaginaria
La unidad imaginaria es √-1 = i
3. Representación gráfica de un número complejo
Un número complejo Z = (a, b) se representa por un vector OP siendo P = (a, b)
El eje horizontal es el eje real. El eje vertical es el eje imaginario.
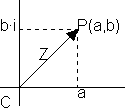
z = (a, b) = a + b·i = OP
4. Formas de expresar un número complejo
- Forma vectorial o par ordenado Z = (a, b)
- Forma binómica Z = a + b·i
- Forma polar Z = rα
El módulo de un número complejo Z es r y es la raíz cuadrada de la suma de los cuadrados de la componente real y la componente imaginaria.
r = √a² + b²
El argumento del número complejo Z es α y es el ángulo que forma el número complejo Z con el eje real (en sentido positivo).
Z = rα
Forma trigonométrica o módulo argumental Z = r·(cos α + i·sen α)
| α = arctg | b |
| a |
5. Números conjugados y opuestos de otro complejo
Dado un complejo Z = a + b·i, su conjugado (Z) tiene la misma parte real y opuesta la parte imaginaria.
Z = a - b·i
El complejo opuesto de Z = a + b·i es -Z y tiene opuestas las componentes real e imaginaria de Z.
Z = -a - b·i
6. Potencias de la unidad imaginaria
i° = 1
i¹ = i = √-1
i² = -1
i³ = -i
i⁴ = 1
Cuando el exponente es superior a 4 se divide entre 4, igualando el enunciado a i elevado al resto de la división.
iⁿ = i4·c + r = i⁴˙ᶜ·ir = (i⁴)ᶜ·ir = (1)ᶜ·ir = 1·ir = ir
c: es el cociente,
r: es el resto de la división,
Ejemplo de potencias de la unidad imaginaria
Si el exponente es "9", entonces:
c = 2
r = 1
i⁹ = i4·2 + 1 = i⁴˙²·i¹ = (i⁴)²·i¹ = (1)²·i¹ = 1·i¹ = i¹ = i
7. Operaciones con números complejos
a) En forma binómica
1. Suma
Z₁ + Z₂ = (a + b·i) + (c + d·i)
Z₁ + Z₂ = (a + c) + (b + d)·i
2. Resta
Z₁ - Z₂ = (a + b·i) - (c + d·i)
Z₁ - Z₂ = (a - c) + (b - d)·i
3. Producto
Z₁·Z₂ = (a + b·i)·(c + d·i)
Z₁·Z₂ = (a·c - b·d) + (b·c + a·d)·i
4. Producto de un número real por un número complejo
k ∈ ℜ
k·Z₁ = k·(a + b·i)
k·Z₁ = k·a + k·b·i
5. Cociente
| Z₁ | = | a + b·i | = | (a + b·i)·(c - d·i) |
| Z₂ | c + d·i | (c + d·i)·(c - d·i) |
| Z₁ | = | (a·c + b·d) + (-a·d + b·c)·i |
| Z₂ | c² - (d·i)² |
| Z₁ | = | (a·c + b·d) + (-a·d + b·c)·i |
| Z₂ | c² + d² |
6. Inverso de un número complejo
| 1 | = | 1 | = | 1·(a - b·i) |
| Z | a + b·i | (a + b·i)·(a - b·i) |
| 1 | = | a | - | b | ·i |
| Z | a² + b² | a² + b² |
7. Potencia de un complejo
Z₁² = (a + b·i)²
Z₁² = a² + (b·i)² + 2·a·b·i
Z₁² = a² + b²·i² + 2·a·b·i
Z₁² = a² - b² + 2·a·b·i
b) En forma polar
1. Producto de complejos
Z₁·Z₂ = (r₁)α1·(r₂)α2
Z₁·Z₂ = (r₁·r₂)α1 + α2
2. Cociente de complejos
| Z₁ | = | (r₁)α1 | = (r₁/r₂)α1 - α2 |
| Z₂ | (r₂)α2 |
3. Potencia de un complejo
Z₁ⁿ = (rα)ⁿ = rⁿ
4. Radicación de un complejo
La raíz enésima de un complejo Z = rα tiene por módulo la raíz enésima de su módulo. Su argumento es:
(α + 360°·k)/n
El número de raíces es n para k = 0; k = 1; … k = n - 1.
![]()
Autor: Angel Ramos. España.
Editor: Ricardo Santiago Netto (Administrador de Fisicanet).
¿Qué son los números complejos y cómo se representan? ¿Cuál es el conjugado de un número complejo? ¿Cuál es el opuesto de un número complejo?