Propiedades de los números complejos II
Los algebristas de los siglos XV y XVI, al buscar una solución para algunas ecuaciones de segundo grado, por ejemplo x² + 1 = 0, se encontraron con x = ±√-1. Afirmaban que las ecuaciones no tenían solución, ya que no hay ningún número real cuyo cuadrado sea un número negativo. Este hecho implicaba la conveniencia de "definir" nuevos números de la forma: a + b·i donde a y b son números reales e i es √-1, que permitieran resolver cualquier ecuación de segundo grado. Estos nuevos números se llaman números complejos (C).
Ejemplo nº 1
La ecuación de segundo grado:
x² - 6·x + 34 = 0
Tiene como solución:
| x = | 6 ± √-100 |
| 2 |
Que expresaremos como:
| x = | 6 ± 10·i | ⇒ x = 3 ± 5·i |
| 2 |
• Definición:
Se llama número complejo a toda expresión de la forma z = a + b·i donde a y b son números reales; i es la unidad llamada imaginaria, definida por las ecuaciones: i = √-1 o i² = -1; a es la parte real y b es la parte imaginaria del número complejo.
Si a = 0, el número complejo 0 + b·i = b·i, es un número imaginario puro; si b = 0, se obtiene el número real a + 0·i = a
Dos números complejos son iguales si: (a + b·i) = (c + d·i) ⇔ a = c; b = d es decir, si son iguales sus partes reales e imaginarias por separado.
Un número complejo es igual a cero si: a + b·i = 0 ⇔ a = 0; b = 0
Representación gráfica
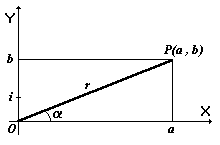
Sobre el eje de abscisas se representa la parte real a del número complejo y sobre el eje de ordenadas la parte imaginaria b. El número complejo (a, b) queda representado por el punto P(a, b) del plano de coordenadas.
A cada número complejo (a, b) corresponde un punto P que se llama su afijo, y recíprocamente, a cada punto corresponde un número complejo. De este modo queda establecida una aplicación biyectiva entre los puntos del plano y los números complejos.
Si escribimos z = (a, b) = (a, 0) + (0, b) y consideramos la relación vectorial correspondiente, podemos escribir: z = a + b·i que llamaremos forma binómica del número complejo z. Cuando aparezca escrito como (a, b) diremos que está en forma cartesiana.
El origen de coordenadas O y el punto P determinan un vector OP que se puede considerar la representación vectorial del número complejo (a, b). La longitud r del vector OP se llama módulo del número complejo a + b·i y su expresión es r = √a² + b²
Complejos conjugados y complejos opuestos
Dos números complejos se llaman conjugados si tienen iguales sus componentes reales y opuestas sus componentes imaginarias. Se expresan de la forma siguiente: z = a + b·i y z = a - b·i. Gráficamente son simétricos respecto del eje real (eje de abscisas).
Dos números complejos se llaman opuestos si tienen opuestas sus dos componentes. Se expresan de la forma siguiente: z = a + b·i y - z = -a - b·i. Gráficamente son simétricos respecto del origen de coordenadas.
Propiedades:
![]() = z
= z
z₁ + z₂ = z₁ + z₂
-z = -(z)
z₁·z₂ = z₁·z₂
z₁÷z₂ = z₁÷z₂
|z|² = z·z
| Re z = | z + z |
| 2 |
| Im z = | z - z |
| 2 |
Forma trigonométrica de un complejo
Designemos por α y r (r ≥ 0) las coordenadas polares del punto P(a, b) tomando por polo el origen de coordenadas y por eje polar, la dirección positiva del eje OX. En este caso tenemos las expresiones siguientes:
| a = r·cos α | ⇒ a + b·i = |
| b = r·sen α |
= (r·cos α) + (r·sen α)·i = r·(cos α + i·sen α)
La expresión r·(cos α + i·sen α) se llama forma trigonométrica del número complejo a + b·i y las magnitudes r y α se expresan en función de a y b mediante las fórmulas:
r = √a² + b²
| tg α = | b | ⇒ α = arctg | b |
| a | a |
El número r se llama módulo y α argumento del número complejo a + b·i. Si α ∈ [0, 2·π [, obtenemos el argumento principal.
Operaciones con números complejos. En forma binómica
Suma y resta:
(a + b·i) ± (c + d·i) = (a ± c) + (b ± d)·i
Producto:
(a + b·i)·(c + d·i) = (a·c - b·d) + (a·d + b·c)·i
En la práctica puedes aplicar la propiedad distributiva teniendo en cuenta que i² = -1
Cociente:
| (a + b·i) | = | a·c + b·d | + | b·c - a·d | ·i |
| (c + d·i) | c² + d² | c² + d² |
En la práctica se multiplica numerador y denominador por el conjugado del denominador
Raíz cuadrada:
Si √a + b·i = x + y·i ⇒ a + b·i = (x + y·i)² = x² - y² + 2·x·y·i
Igualando las partes real e imaginaria resulta el sistema:
| x² - y² = a |
| 2·x·y = b |
Resolviendo el sistema se tiene la solución.
Operaciones con números complejos. En forma trigonométrica
Producto:
Sean:
z₁ = r₁·(cos α + i·sen α)
z₂ = r₂·(cos β + i·sen β)
Multiplicando:
z₁·z₂ = r₁·r₂·[cos (α + β) + i·sen (α + β)]
El módulo del cociente es el cociente de los módulos.
Un argumento del cociente es la diferencia de los argumentos.
Cociente:
Sean:
z₁ = r₁·(cos α + i·sen α)
z₂ = r₂·(cos β + i·sen β)
Dividiendo:
| z₁ | = | r₁ | ·[cos (α - β) + i·sen (α - β)] |
| z₂ | r₂ |
El módulo del cociente es el cociente de los módulos.
Un argumento del cociente es la diferencia de los argumentos.
Operaciones con números complejos. En forma polar
La forma trigonométrica de un complejo sugiere que éste quede perfectamente determinado por su módulo r y un argumento α.
Si escribimos rα = r·(cos α + i·sen α) también tenemos una expresión que pone de manifiesto los valores del módulo y un argumento. Se le conoce por forma polar de un número complejo.
El producto en forma polar quedaría:
rα·sᵦ = (r·s)α + β ⇒ como consecuencia (rα)ⁿ = (rⁿ)ₙ.ᵦ
El cociente en forma polar quedaría:
rα/sᵦ = (r/s)α - β
Forma De Moivre para el producto
| z₁·z₂· … ·zₙ = (r₁·r₂· … ·rₙ)·(cos | n ∑ k = 1 | αₖ + i·sen | n ∑ k = 1 | αₖ) |
Forma De Moivre para la potencia
zⁿ = rⁿ·[cos (n·α) + i·sen (n·α)]
Consecuencia:
Considerando un complejo de módulo la unidad:
(cos α + i·sen α)ⁿ = (cos n·α + i·sen n·α) y desarrollando el primer miembro según la fórmula del binomio de Newton e igualando las partes reales e imaginarias, podremos expresar sen n·α y cos n·α en función de sen α y cos α.
Raíces n-ésimas de un complejo
Definición:
z₁ es una raíz n-ésima de z si z₁ⁿ = z
Teorema:
Todo complejo z ≠ 0 tiene exactamente n raíces n-ésimas distintas en C.
Sea z = R·(cos Φ + i·sen Φ) un complejo no nulo.
Supongamos que r·(cos α + i·sen α) es una de sus raíces n-ésimas.
Deberá verificarse:
[(cos α + i·sen α)]ⁿ = R·(cosΦ + i·sen Φ),
es decir;
rⁿ·(cos n·α + i·sen n·α) = R·(cosΦ + i·sen Φ)
Deberán coincidir los módulos:
rⁿ = R ⇒ r = ⁿ√R (su valor aritmético, real y positivo)
Para que los complejos de módulo unidad cos n·α + i·sen n·α coincidan, n·α y Φdeberán ser dos argumentos del mismo complejo. En otras palabras, n·α = Φ + 2·k·π de donde: α = (Φ + 2·k·π)/n
Resumiendo: las raíces n-ésimas de z son de la forma:
| ⁿ√R·(cos | Φ + 2·k·π | + i·sen | Φ + 2·k·π | ) k ∈ Z (k = 0, 1, 2, …, n - 1) |
| n | n |
La raíz n-ésima de número real A, distinto de cero, también tiene n valores, puesto que en número real es un caso particular del número complejo y puede ser representado en forma trigonométrica:
Si A > 0, A = |A|·(cos 0 + i·sen 0)
Si A < 0, A = |A|·(cos π + i·sen π)
Interpretación geométrica de las raíces n-ésimas de z
Se observa que todas las raíces tienen el mismo módulo: ⁿ√R. Por ello, los afijos de la n raíces están situados sobre la circunferencia de centro el origen y radio ⁿ√R.
Si Φ es un argumento de z, un argumento de z₁ es Φ/n. Si dividimos los 2·π radianes en n partes, cada una de ellas mide 2·π/n radianes.
Así el afijo de z₂ se obtiene girando el de z₁ en 2·π/n radianes; el de z₃ girando el de z₂ otra vez un ángulo de 2·π/n radianes, y así sucesivamente.
Ver resolución de la ecuación binomia
La ecuación xⁿ = A se llama binomia. Las raíces de esta ecuación serán:
Si A es un número real positivo:
| x = ⁿ√A·(cos | 2·k·π | + i·sen | 2·k·π | ) |
| n | n |
Si A es un número real negativo:
| x = ⁿ√|A|·(cos | π + 2·k·π | + i·sen | π + 2·k·π | ) |
| n | n |
Si A es un número complejo, los valores de x se hallan según la expresión general.
Función exponencial de exponente complejo y sus propiedades
Sea z = x + y·i, si x e y son variables reales, z es una variable compleja. Consideremos la función exponencial de variable compleja:
f(z) = ez = ex + y·i
Los valores complejos de la función f(z) se definen del modo siguiente:
ex + y·i = eˣ·(cos α + i·sen α)
Propiedades:
Sean z, z₁ y z₂ números complejos y m un número entero, entonces:
| (ez)ᵐ = em·z | ez + 2·π·i = ez |
Se cumplen las reglas de derivación de la función exponencial de variable real.
Fórmula de Euler. Forma exponencial de un número complejo
Consideremos un número imaginario puro, la fórmula de Euler expresa la relación entre la función exponencial de exponente imaginario y las funciones trigonométricas y es: eʸ˙ⁱ = cos α + i·sen α de la podemos deducir las expresiones de seno y coseno en función de ellas.
| eʸ˙ⁱ = cos y + i·sen y | ⇒ | cos y = | eʸ˙ⁱ + e⁻ʸ˙ⁱ | ||
| 2 | |||||
| e⁻ʸ˙ⁱ = cos y - i·sen y | sen y = | eʸ˙ⁱ - e⁻ʸ˙ⁱ | |||
| 2·i | |||||
Forma exponencial de un número complejo:
Sea z un número complejo en forma trigonométrica: z = r·(cos α + i·sen α) donde r es el módulo y α un argumento. Según la fórmula de Euler: cos α + i·sen α = eα·i ⇒ z = r·eα·i y todo número complejo puede ser representado en forma exponencial.
Logaritmos de números complejos
Sea z un número complejo, por definición de logaritmo tenemos:
ln z = w ⇔ ew = z
Si z = r·(cos α + i·sen α) y w = x + y·i:
ex + y·i = r·(cos α + i·sen α)
eˣ·(cos y + i·sen y) = r·(cos α + i·sen α)
| ⇒ | eˣ = r ⇒ x = ln r = ln |z| |
| y = arg z + 2·k·π |
Luego:
ln z = ln |z| + (arg z + 2·k·π)·i, k ∈ Z;
Para k = 0 tenemos el valor principal:
ln z = ln |z| + i·arg z
Ejemplo nº 2
ln (3 + 4·i) = 1,60944 + (0,2 + 2·k·π)·i
Potencia de base y exponente complejo
Sean z y w ∈ C, con z ≠ 0. Se define zw = ew·ln z
Autor: Francisco Merchan. España.
Editor: Ricardo Santiago Netto (Administrador de Fisicanet).
¿Qué son los números complejos y cómo se representan?