Problemas nº 2-u y 2-v de racionalización de denominadores - TP09
Enunciado de los ejercicios nº 2-u y 2-v
Racionalizar los denominadores de las siguientes fracciones:
| u) | 1 - 2·√2 | = |
| 2·√2 - √7 + 2·√2 |
| v) | 1 | = |
| √a + √b + √c |
Solución
Multiplicamos y dividimos la fracción por el radical que haga "1" al exponente fraccionario del denominador:
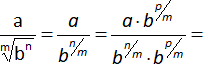
Siendo:
n + p = m
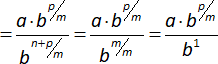
u)
| 1 - 2·√2 | = |
| 2·√2 - √7 + 2·√2 |
En el denominador podemos una formar diferencia de cuadrados con el binomio:
2·√2 + √7 + 2·√2
Multiplicamos numerador y denominador por el binomio propuesto:
| = | (1 - 2·√2)·(2·√2 + √7 + 2·√2) | = |
| (2·√2 - √7 + 2·√2)·(2·√2 + √7 + 2·√2) |
| = | (1 - 2·√2)·(2·√2 + √7 + 2·√2) | = |
| (2·√2)² - (√7 + 2·√2)² |
| = | (1 - 2·√2)·(2·√2 + √7 + 2·√2) | = |
| 4·2 - (7 + 2·√2) |
| = | (1 - 2·√2)·(2·√2 + √7 + 2·√2) | = |
| 8 - 7 - 2·√2 |
| = | (1 - 2·√2)·(2·√2 + √7 + 2·√2) | = |
| 1 - 2·√2 |
Simplificamos:
= 2·√2 + √7 + 2·√2
Expresamos el resultado:
| 1 - 2·√2 | = 2·√2 + √7 + 2·√2 |
| 2·√2 - √7 + 2·√2 |
v)
| 1 | = |
| √a + √b + √c |
En el denominador podemos formar diferencias de cuadrados en grupos con el binomio:
√a - (√b + √c)
Multiplicamos numerador y denominador por el binomio propuesto:
| = | 1·[√a - (√b + √c)] | = |
| [√a + (√b + √c)]·[√a - (√b + √c)] |
| = | √a - √b + √c | = |
| (√a)² - (√b + √c)² |
| = | √a - √b + √c | = |
| a - [(√b)² + 2·√b·√c + (√c)²] |
| = | √a - √b + √c | = |
| a - (b + 2·√b·c + c) |
| = | √a - √b + √c | = |
| a - b - 2·√b·c - c |
| = | √a - √b + √c | = |
| a - b - c - 2·√b·c |
Nuevamente aplicamos diferencia de cuadrados en grupo en el numerador y en el denominador:
| = | (√a - √b + √c)·[(a - b - c) + 2·√b·c] | = |
| [(a - b - c) - 2·√b·c]·[(a - b - c) + 2·√b·c] |
| = | (√a - √b + √c)·(a - b - c + 2·√b·c) | = |
| a² - a·b - a·c - a·b + b² + b·c - a·c + b·c + c² - 4·b·c |
| = | (√a - √b + √c)·(a - b - c + 2·√b·c) | = |
| a² - 2·a·b - 2·a·c + b² + 2·b·c + c² - 4·b·c |
| = | (√a - √b + √c)·(a - b - c + 2·√b·c) |
| a² - 2·a·b - 2·a·c + b² + c² - 2·b·c |
Expresamos el resultado:
| 1 | = | (√a - √b + √c)·(a - b - c + 2·√b·c) |
| √a + √b + √c | a² - 2·a·b - 2·a·c + b² + c² - 2·b·c |
Resolvió: Ricardo Santiago Netto. Argentina
- ‹ Anterior |
- Regresar a la guía TP09
- | Siguiente ›
Ejemplo, como racionalizar denominadores