Sistemas de ecuaciones. Aplicaciones lineales
- Concepto y representación
- Resolución de sistemas
- Tipos de sistemas
- Teorema Rouche-Frobenius
- Regla de Cramer
- Sistemas homogéneos
- Por descomposición L U
Concepto y representación
Llamaremos sistema de m ecuaciones con n-incógnitas a toda expresión:
a₁₁·x₁ + a₁₂·x₂ + … + a₁ₙ·xₙ = b₁
a₂₁·x₁ + a₂₂·x₂ + … + a₂ₙ·xₙ = b₂
…………………
aₘ₁·x₁ + aₘ₂·x₂ + … + aₘₙ·xₙ = bₘ
Donde:
aij ∈ K: Son los coeficientes.
bᵢ ∈ K: Son los términos independientes.
xᵢ: Son las incógnitas.
a)
Se puede representar de forma Matricial:
A·X = B
Donde:
A: Matriz de los coeficientes.
X: Vector solución.
B: Vector de Términos Independientes.
A*: Resulta de añadir los términos independientes a la matriz A.
b)
También de forma vectorial:
x₁·A₁ + x₂·A₂ + … + xₙ·Aₙ = B (donde Aᵢ son las columnas de A)
c)
Como una aplicación lineal
Sabiendo que toda matriz de dimensión m×n define una aplicación lineal f:Kⁿ Kᵐ respecto de las bases canónicas de Kⁿ y Kᵐ
Podemos entender un sistema de m ecuaciones y n-incógnitas, como una aplicación lineal coeficientes de las distintas incógnitas ∈ Kⁿ
Simplificación
Si a un sistema de ecuaciones se le añade un número finito de ecuaciones lineales que son combinaciones lineales de las dadas, el nuevo sistema es equivalente al inicial.
Del mismo modo si eliminamos una ecuación que sea combinación lineal de otra se puede eliminar.
Ver resolución del sistema
Si (α₁, α₂, …, αₙ) satisface las m ecuaciones decimos que α es el vector solución del sistema.
Según el número de soluciones un sistema puede ser:
Sistema homogéneo: Si los términos independientes son cero.
Sistema incompatible: Si el sistema no tiene solución.
Sistema compatible determinado: Si el sistema posee una una solución.
Sistema compatible indeterminado: Si el sistema posee infinitas soluciones.
Si dos sistema tienen las mismas soluciones son equivalentes
Si A·x = b un sistema de ecuaciones podemos ver la matriz A como asociada a una aplicación lineal f.
Resolver el sistema es hallar f⁻¹(b) = x + Ker f donde f(x) = b.
| 1 | 0 | 0 | 0 | · | x | = | 0 | ||||||
| 1 | 0 | -1 | a | y | 0 | ||||||||
| 3 | 0 | -1 | a | z | 0 | ||||||||
| b | 0 | 0 | 1 | t | 0 |
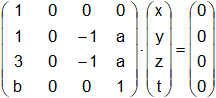
Ejemplo: Obtener una base del espacio vectorial solución del sistema:
x + 0·y + 0·z + 0·t = 0
x + 0·y - 1·z + a·t = 0 ⇒ x = 0 ⇒ (x, y, z, t) = (0, y, 0, 0)
3·x + 0·y - 1·z + a·t = 0 ⇒ t = 0
b·x + 0·y + 0·z + 1·t = 0 ⇒ z = 0
La solución es < (0, 1, 0, 0) > que es base del espacio vectorial formado por las soluciones.
Teorema Rouche-Frobenius
Dado A·x = b un sistema de m ecuaciones con n-incógnitas, tiene solución si:
rango A = rango A* = número de incógnitas (n) ⟶ S. C. Determinado.
rango A = rango A* < número de incógnitas (n) ⟶ S. C. Indeterminado.
rango A < rango A* ⟶ S. Incompatible.
Regla de Cramer
Dado un sistema compatible determinado, tenemos que:
Su expresión matricial es AX = B y al ser rango A = n ⇒ |A| ≠ 0 y además A tiene inversa A⁻¹. Así pues:
A⁻¹·A·X = A⁻¹·B ⇒ I·X = A⁻¹·B ⇒ X = A⁻¹·B ⇒ X = (1/|A|·At)·B ⇒
⇒ xᵢ = 1/|A|·(A₁ᵢ b₁ + A₂ᵢ b₂ + … + Aₙᵢ bₙ)
De donde obtenemos la Regla de Cramer:
| det (B, C₂, C₃, …, Cₙ) | det (C₁, B, C₃, …, Cₙ) | det (C₁, C₂, C₃, …, B) | ||
| x₁ = | , | x₂ = | , …… | xₙ = |
| det |A| | det |A| | det |A| |
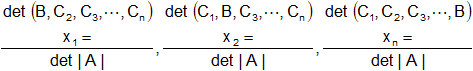
Si el sistema es compatible indeterminado podemos resolverlo por Cramer:
- Pasamos una de las incógnitas a la matriz de los términos independientes en cada ecuacion
- Resolvemos el sistema por Cramer, y nos daran las soluciones en función de esa incognita
- Expresamos la solución en forma de envoltura lineal
Ejemplo: Resolver el sistema por Cramer.
x + y + z = 1
x - y + 3·z = 3
x + y = 1 - λ
x - y = 3 - 3·λ
| A = | 1 | 1 | ||
| 1 | -1 |
| A* = | 1 | 1 | (1 - λ) | ||
| 1 | -1 | (3 - 3·λ) |
Cambiamos z por λ y pasamos λ a la derecha.
Resolvemos el sistema por Cramer y obtenemos:
x = -2·λ + 2 de modo que la solución es {(-2·λ + 2, -1 + λ, λ); λ ∈ ℜ} ⇒ {(2, -1, 0) + (-2·λ, λ, λ); λ ∈ ℜ}
y = -1 + λ
Y por ultimo extrayendo λ tenemos que las infinitas soluciones del sistema son:
{(2, -1, 0) + < (-2, 1, 1) >}
Sistemas homogéneos
Un sistema homogéneo siempre posee, al menos, la solución trivial (x, y, z, t …) = (0, 0, 0 … 0).
Por el teorema de Rouche podemos afirmar que siempre es compatible, ya que rango A = rango A*×Ax = 0
Si rango A = rango A* = n es S.C. Determinado con la solución trivial como única solución.
Si rango A = rango A* < n es S.C. Indeterminado cuyas soluciones son los valores que anulan la ecuación.
Es decir, los valores de las incógnitas para los cuales f es cero (Ker f).
Un sistema homogéneo siempre se puede expresar con n ecuaciones con n-incógnitas. De modo que si faltan ecuaciones (ecuaciones < incógnitas) se añaden combinaciones lineales y si sobran (ecuaciones > incógnitas) entonces se eliminan porque alguna ecuación será combinación lineal.
Ejemplo: Resolver el siguiente sistema homogéneo:
x + y + z = 0
2·x + 2·y +2·z = 0
x + y - z = 0
3·x + 3·y + z = 0
Primero eliminamos la segunda ecuación porque es proporcional a la primera.
| 1 | 1 | 1 | = 0 | ||
| 1 | 1 | -1 | |||
| 3 | 3 | 1 |
rg(A) < 3
Hallamos el determinante de A para saber el rango
Como C₁ = C₂ el rango es dos. Y al ser homogéneo rango A = rango A* = 2 < n-incógnitas ⇒ S.C.I
Si resolvemos el sistema por igualación tenemos x = -y por lo que la solución es {(x, -x, 0): ∈ ℜ}
O lo que es lo mismo {< (1, -1, 0) >} = Ker (f) si tomamos el sistema como la ap. lineal f.
Método de Gauss
Consiste en transformar un sistema Ax = B en un sistema triangular Ux = c realizando operaciones elementales de Gauss en la matriz ampliada A*. El sistema triangular obtenido es equivalente al inicial.
Si al reducir por Gauss llegaramos a un absurdo como 0 = 1 el sistema inicial era incompatible.
Ejemplo: Resolvemos el sistema anterior por Gauss
x + y + z = 0
x + y - z = 0
| 1 | 1 | 1 | e₁ - e₂ ⟶ | 1 | 1 | 1 | 3·e₁ - e₃ ⟶ | 1 | 1 | 1 | e₃ - e₂ ⟶ | 1 | 1 | 1 | ||||||||
| 1 | 1 | -1 | 0 | 0 | 2 | 0 | 0 | 2 | 0 | 0 | 2 | |||||||||||
| 3 | 3 | 1 | 3 | 3 | 1 | 0 | 0 | 2 | 0 | 0 | 0 |
3·x + 3·y + z = 0
x + y + z = 0 ⇒ z = 0 ⇒ x = -y
Solución: < (x, -x, 0) >; x ∈ ℜ
Por descomposición LU
Dado un sistema A·x = B siendo A una matriz cuadrada (incógnitas = ecuaciones) podemos encontrar la descomposición LU de la matriz A de modo que A = L·U (producto de una matriz triangular inferior y una superior).
A·x = B ⇔ L·Ux = B ⇔ Ux = y
Ly = B
La solución se obtiene resolviendo dos sistemas triangulares, se resuelve Ly = B y una vez tenemos el vector y hallamos x, las componentes de x con las incógnitas x, y, z, t …
Este metodo es util para la resolución se sistemas simultáneos, es decir, que con una sola descomposición LU podemos hallar las soluciones de un mismo sistema para cualquier valor que tomen sus términos independientes (cambiando B).
Editor: Ricardo Santiago Netto (Administrador de Fisicanet).
¿Cuál es la regla de Cramer?