Sistemas de ecuaciones. Métodos y ejercicios

Métodos para la resolución de sistemas de ecuaciones

1) Método de reducción por suma o resta (o de eliminación)

2) Método de igualación

3) Método de sustitución

Método de reducción por suma o resta (o de eliminación).

Ejemplo:

6·x - 7·y = 5
8·x - 9·y = 7

1^er Paso: Multiplicamos las 2 ecuaciones por un "número" (resultado del m.c.m. entre ellos), para igualar el valor numérico de los coeficientes de la incógnita x en las 2 ecuaciones.

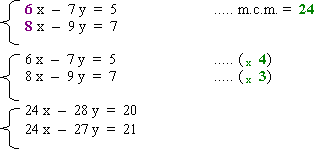
2^do Paso: Restamos las 2 ecuaciones para eliminar las incógnitas x luego resolvemos la ecuación.

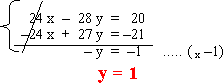
3^er Paso: Reemplazamos la incógnita y, en cualquiera de las 2 ecuaciones para obtener el valor de la incógnita x o bien se calcula está incógnita repitiendo los pasos anteriores.

6·x - 7·y = 5

6·x - 7·(1) = 5

6·x - 7 = 5

6·x = 5 + 7

6·x = 12

x = 2

Por último; el conjunto solución es: (2; 1)

Ejercicios de aplicación

2·x - 4·y = -7
x + 8·y = -1

• R: [-3; ¼]

3·x - 5·y = 19
2·x + y = 4

• R: [3; -2]

5·x + 4·y = 2
3·x - 2·y = -12

• R: [-2; 3]

-9·x - 12·y = 14
30·x + 6·y = -58

• R: [-2; ⅓]

2·x - 5·y/3 = 5
3·x - 4·y = 3

• R: [5; 3]

2·x - 2·y = -5
4·x - 3·y = -9

• R: [-3/2; 1]

x + y = 7
x - y = -1

• R: [3; 4]

x - y/5 = 9/5
2·x + y/2 = 9/2

• R: [2; 1]

-2·x - 4·y = 18
x + 5·y = -36

• R: [9; -9]

2·x/3 - 5·y = -55/3
3·x - y/2 = -33/2

• R: [-5; 3]

3·x - 3·y = -14
9·x + 4·y = 23

• R: [⅓; 5]

2·x - 5·y = -9
x + 4·y = 8,5

• R: [½; 2]

x - 5·y = -14,5
2·x + 3·y = 10

• R: [½; 3]

5·x - 6·y = 34
11·x + 9·y = -14

• R: [2; -4]

Método de igualación.

Ejemplo:

x + 3·y = 10
2·x + 5·y/4 = 1

1^er Paso: Se despeja la incógnita x de cada una de las ecuaciones dadas.

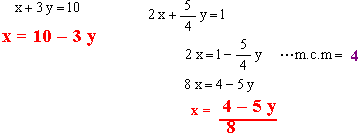
2^do Paso: Igualamos las incógnitas x luego resolvemos la ecuación.

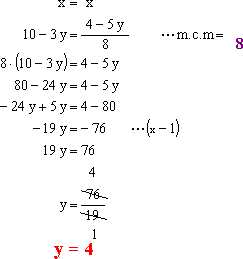
3^er Paso: Reemplazamos la incógnita y, en cualquiera de las 2 ecuaciones despejadas para obtener el valor de la incógnita x.

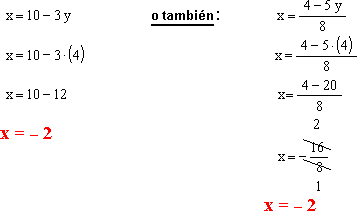
Por último; el conjunto solución es: (- 2; 4).

Ejercicios de aplicación

5·x - y = 9
2·x + 4·y = 8

• R: [2; 1]

5·x - y = ½
2·x + 3·y = -10

• R: [-½; -3]

2·x - 4·y = -7
x + 8·y = -1

• R: [-3; ¼]

-3·x + 15·y = 59
3·x + 4·y = 17

• R: [⅓; 4]

-3·x - 4·y = 5
-x - 2·y = 2

• R: [-1; -½]

3·x - 5·y = 19
2·x + y = 4

• R: [3; -2]

x/5 - y/2 = 1,3
2·x - y = 1

• R: [-1; -3]

3·x - y = -½
4·x/5 + 3·y = 6,4

• R: [½; 2]

2·x - y/2 = -9,5
3·x/5 + y = -4

• R: [-5; -1]

x/3 - y = -3
-4·x - y/2 = 11

• R: [-3; 2]

3·x + 2·y = -10
2·x - 10·y = -1

• R: [-3; -½]

3·x - 2·y = 5
-3·x + 4·y = -9

• R: [⅓; -2]

Método de sustitución

Ejemplo:

x + 2·y = 9
3·x - y = 13

1^er Paso: Se despeja la incógnita x de una de las ecuaciones dadas.

x + 2·9

x = 9 - 2·y

2^do Paso: Reemplazamos la incógnita x, en la otra ecuación dada; para obtener el valor de la incógnita y.

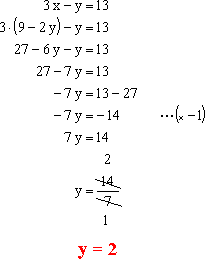
3^er Paso: Reemplazamos la incógnita y, en la 1^ra expresión obtenida; para obtener el valor de la incógnita x.

x = 9 - 2·y

x = 9 - 2·(2)

x = 9 - 4

x = 5

Por último; el conjunto solución es: (5; 2).

Ejercicios de aplicación

2·x - 3·y = 5
3·x - 2·y = 5

• R: [1; -1]

x/5 - 2·y = 10
3·x - 3·y/2 = 36

• R: [10; -4]

2·x + y = 3
1,5·x - 2·y = 5

• R: [2; -1]

x + 8·y = 3
3·x - y = -28,5

• R: [-9; 3/2]

2·x - 5·y/3 = 5
3·x - 4·y = 3

• R: [5; 3]

2·x - 4·y = 5
3·x + y = 5,75

• R: [2; -¼]

5·x + 6·y = 32
3·x - 2·y = -20

• R: [-2; 7]

x + 2·y = -12
3·x - y = -1

• R: [-2; -5]

6·x + 3·y = 3,5
5·x - 2·y = ⅔

• R: [⅓; ½]

3·x/2 + y = 8
2,5·x - 3·y/2 = 7

• R: [4; 2]

5·x - 6·y = -9
3·x + 4·y = -13

• R: [-3; -1]

4·x - 3·y = -41
6·x + 11·y = 47

• R: [-5; 7]

Autor: Hugo David Giménez Ayala. Paraguay.

Editor: Ricardo Santiago Netto (Administrador de Fisicanet).

¿Qué es el método de igualación? ¿Qué es un sistema de ecuaciones con dos incógnitas? ¿Qué es el método de sustitución?