Análisis de regresión y correlación (segunda parte)
Análisis de Regresión
- Objetivo: determinar la ecuación de regresión para predecir los valores de la variable dependiente (Y) en base a la o las variables independientes (X)
- Procedimiento: seleccionar una muestra a partir de la población, listar pares de datos para cada observación; dibujar un diagrama de puntos para dar una imagen visual de la relación; determinar la ecuación de regresión
Supuestos de Regresión Lineal Clásica
• Cada error está normalmente distribuido con:
- Esperanza de los errores igual a 0
- Variancia de los errores igual a una constante σ²
- Covariancia de los errores nulas para todo i ≠ Ψ
Proceso de estimación de la regresión lineal simple
Modelo de regresióny = β₀ + β₁x + ε Ecuación de regresiónE(y) = β₀ + β₁·x Parámetros desconocidosβ₀·β₁ | Datos de la muestra.
| ||||
b₀ y b₁ Proporcionan estimados β₀ y β₁ | Ecuación estimada de regresióny = b₀ + b₁·x Estadísticos de la muestrab₀·b₁ |
Líneas posibles de regresión en la regresión lineal simple
Sección A

Relación lineal positiva
Sección C
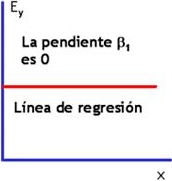
No hay relación
Sección B

Relación lineal negativa
Estimación de la ecuación de regresión simple
Y' = a + b·X, donde:
- Y' es el valor estimado de Y para distintos X
- a es la intersección o el valor estimado de Y cuando X = 0
- b es la pendiente de la línea, o el cambio promedio de Y' para cada cambio en una unidad de X
- El principio de mínimos cuadrados es usado para obtener a y b:
| b = | n·(∑X·Y) - (∑X)·(∑Y) |
| n·(∑X²) - (∑X)² |
| a = | ∑Y - b·(∑X) |
| n |
Mínimos cuadrados - supuestos
El modelo de regresión es lineal en los parámetros.
Los valores de X son fijos en muestreo repetido.
El valor medio de la perturbación εi es igual a cero.
Homocedasticidad o igual variancia de εᵢ
No autocorrelación entre las perturbaciones.
La covariancia entre εᵢ y Xᵢ es cero.
El número de observaciones n debe ser mayor que el número de parámetros a estimar.
Variabilidad en los valores de X.
El modelo de regresión está correctamente especificado.
No hay relaciones lineales perfectas entre las explicativas.
Estimación de la variancia de los términos del error (σ²)
Debe ser estimada por varios motivos.
Para tener una indicación de la variabilidad de las distribuciones de probabilidad de Y.
Para realizar inferencias con respecto a la función de regresión y la predicción de Y.
La lógica del desarrollo de un estimador de σ² para el modelo de regresión es la misma que cuando se muestrea una sola población.
La variancia de cada observación Yᵢ es σ², la misma que la de cada término del error
Dado que los Yᵢ provienen de diferentes distribuciones de probabilidades con medias diferentes que dependen del nivel de X, la desviación de una observación Yᵢ debe ser calculada con respecto a su propia media estimada Yᵢ.
Yᵢ - Ŷᵢ = eᵢ
Por tanto, las desviaciones son los residuales.
Y la suma de cuadrados es:
| SCₑ = | n ∑ i = 1 | (Yᵢ - Ŷᵢ)² |
| SCₑ = | n ∑ i = 1 | (Yᵢ - a - b·Xᵢ)² |
| SCₑ = | n ∑ i = 1 | eᵢ² |
La suma de cuadrados del error, tiene n - 2 grados de libertad asociados con ella, ya que se tuvieron que estimar dos parámetros.
Por lo tanto, las desviaciones al cuadrado dividido por los grados de libertad, se denomina cuadrados medios:
| CMₑ = | SCₑ |
| n - 2 |
| n ∑ i = 1 | eᵢ² | |
| CMₑ = | ||
| n - 2 | ||
Donde CM es el cuadrado medio del error o cuadrado medio residual. Es un estimador insesgado de σ²
Análisis de variancia en el análisis de regresión
El enfoque desde el análisis de variancia se basa en la partición de sumas de cuadrados y grados de libertad asociados con la variable respuesta Y.
La variación de los Yᵢ se mide convencionalmente en términos de las desviaciones
(Yᵢ - Yᵢ)
La medida de la variación total SCtot, es la suma de las desviaciones al cuadrado
∑(Yᵢ - Yᵢ)²
Desarrollo formal de la partición
Consideremos la desviación
(Yᵢ - Yᵢ)
Podemos descomponerla en
| (Yᵢ - Y) | = | (Ŷᵢ - Y) | + | (Yᵢ - Ŷᵢ) |
| T | R | E |
(T): desviación total
(R): es la desviación del valor ajustado por la regresión con respecto a la media general
(E): es la desviación de la observación con respecto a la línea de regresión
Si consideremos todas las observaciones y elevamos al cuadrado para que los desvíos no se anulen
| ∑(Yᵢ - Y)² | = | ∑(Ŷᵢ - Y)² | + | ∑(Yᵢ - Ŷᵢ)² |
| SCtot | SCreg | SCₑᵣ |
(SCtot): Suma de cuadrados total
(SCreg): Suma de cuadrados de la regresión
(SCₑᵣ): Suma de cuadrados del error
Dividiendo por los grados de libertad, (n - 1), (k) y (n - 2), respectivamente cada suma de cuadrados, se obtienen los cuadrados medios del análisis de variancia.
Coeficiente de Determinación
Coeficiente de Determinación, R2 - es la proporción de la variación total en la variable dependiente Y que es explicada o contabilizada por la variación en la variable independiente X.
El coeficiente de determinación es el cuadrado del coeficiente de correlación, y varia entre 0 y 1.
Cálculo del R² a través de la siguiente fórmula.
R² = [∑(Ŷc - Y)²]/[∑(Ŷ₀ - Y)²]
Inferencia en Regresión
Los supuestos que establecimos sobre los errores nos permiten hacer inferencia sobre los parámetros de regresión (prueba de hipótesis e intervalos de confianza), ya que los estimadores de β₀ y β₁ pueden cambiar su valor si cambia la muestra.
Por lo tanto debemos conocer la distribución de los estimadores para poder realizar prueba de hipótesis e intervalos de confianza.
Ejemplo: Se desean comparar los rendimientos predichos a partir de la información obtenida por 3 sensores sobre los rendimientos reales por parcelas de lotes de maíz. Los rendimientos (Y) y el los rindes predichos de 4 sensores se presentan a continuación:
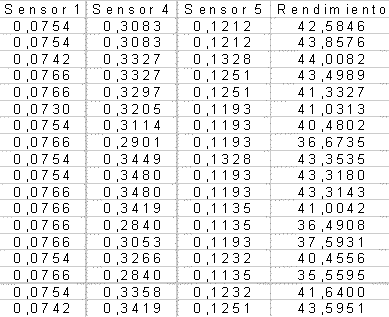
¿Qué sensor refleja mejor el rendimiento de esa zona?
Solución
Descripción gráfica y cuantitativa de la relación entre cada sensor y el rendimiento
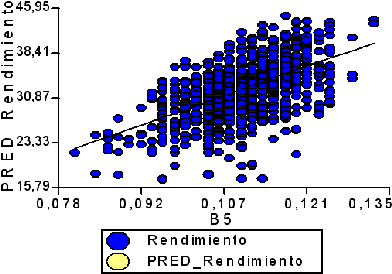
Y = 338,71·X - 4,87
R² = 0,32
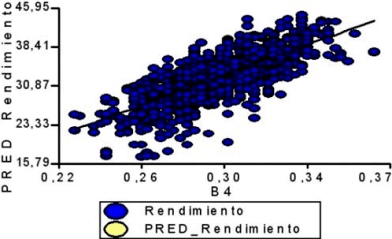
Y = 155,37·X - 13,25
R² = 0,57
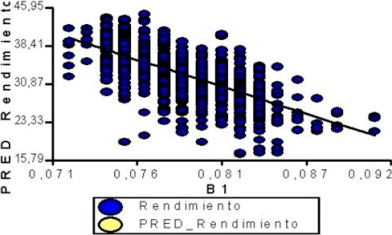
Y = -1004,34·X +112,24
R² = 0,44
Autor: Olga Susana Filippini. Argentina.
Editor: Ricardo Santiago Netto (Administrador de Fisicanet).
- ‹ Anterior
- |
- Siguiente ›
¿Qué es la correlación y regresión?