Análisis de regresión y correlación (primera parte)
Introducción
Muchas veces las decisiones se basan en la relación entre dos o más variables. Ejemplos:
- Dosis de fertilizantes aplicadas y rendimiento del cultivo
- La relación entre la radiación que reciben los sensores con la que se predicen los rendimientos por parcelas con los rendimientos reales observados en dichas parcelas
- Relación entre tamaño de un lote de producción y horas-hombres utilizadas para realizarlo
Distinguiremos entre relaciones funcionales y relaciones estadísticas.
Relación funcional entre dos variables
Una relación funcional se expresa mediante una función matemática.
Si X es la variable independiente e Y es la variable dependiente, una relación funcional tiene la forma:
Y = f(X)
Ejemplo nº 1
| Parcela | Dosis | Rendimiento (kg/h) |
|---|---|---|
| 1 2 3 | 75 25 130 | 150 50 260 |
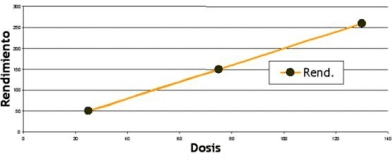
Figura 1: Relación funcional perfecta entre dosis y rendimientos
• Nota: Las observaciones caen exactamente sobre la línea de relación funcional
Relación estadística entre dos variables
A diferencia de la relación funcional, no es una relación perfecta, las observaciones no caen exactamente sobre la curva de relación entre las variables
Ejemplo nº 2
| Lote de productos | Tamaño del lote | Horas hombre |
|---|---|---|
| 1 2 3 4 5 | 30 20 60 80 40 | 73 50 128 170 87 |
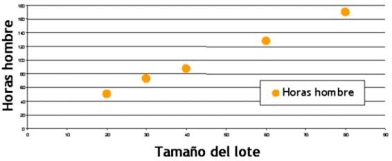
Figura 2: Relación estadística entre tamaño del lote y horas hombre
• Nota: La mayor parte de los punto no caen directamente sobre la línea de relación estadística.
Esta dispersión de punto alrededor de la línea representa la variación aleatoria.
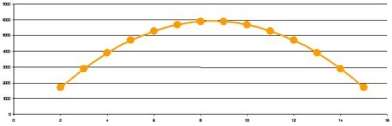
Figura 3: Coordenadas de puntos de control utilizados para corregir la columna de los niveles digitales de una imagen satelital
• Nota: se trata de un terreno rugoso donde varían notablemente las condiciones de observación del sensor, para corregir errores geométricos de la imagen, se aplican funciones de segundo grado. Los datos sugieren que la relación estadística es de tipo curvilínea.
Conceptos básicos
Análisis de Regresión: Es un procedimiento estadístico que estudia la relación funcional entre variables. Con el objeto de predecir una en función de la/s otra/s.
Análisis de Correlación: Un grupo de técnicas estadísticas usadas para medir la intensidad de la relación entre dos variables
Diagrama de Dispersión: Es un gráfico que muestra la intensidad y el sentido de la relación entre dos variables de interés.
Variable dependiente (respuesta, predicha, endógena): es la variable que se desea predecir o estimar
Variables independientes (predictoras, explicativas exógenas). Son las variables que proveen las bases para estimar.
Regresión simple: interviene una sola variable independiente
Regresión múltiple: intervienen dos o más variables independientes.
Regresión lineal: La función es una combinación lineal de los parámetros.
Regresión no lineal: La función que relaciona los parámetros no es una combinación lineal
Gráfico de dispersión
Los diagramas de dispersión no sólo muestran la relación existente entre variables, sino también resaltan las observaciones individuales que se desvían de la relación general. Estas observaciones son conocidas como outliers o valores inusitados, que son puntos de los datos que aparecen separados del resto.
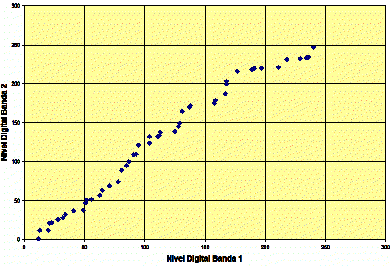
Gráfico de dispersión entre bandas
Coeficiente de correlación lineal
El Coeficiente de Correlación (r) requiere variables medidas en escala de intervalos o de proporciones
- Varía entre -1 y 1
- Valores de -1 ó 1 indican correlación perfecta
- Valor igual a 0 indica ausencia de correlación
- Valores negativos indican una relación lineal inversa y valores positivos indican una relación lineal directa
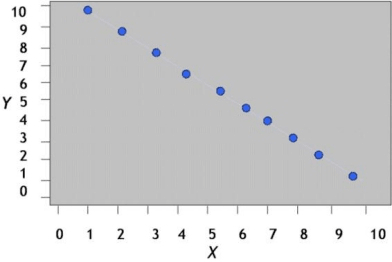
Gráfico de una correlación negativa perfecta
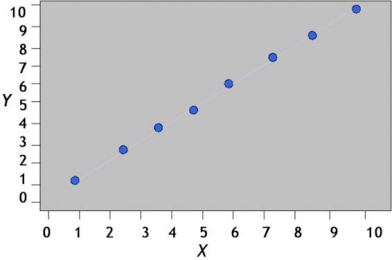
Gráfico de una correlación positiva perfecta
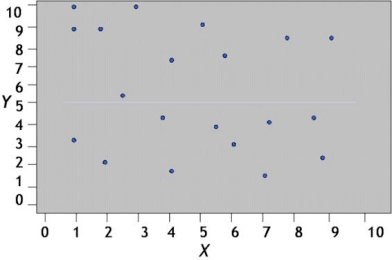
Ausencia de correlación
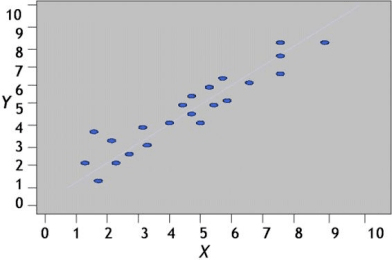
Correlación fuerte y positiva
Fórmula para el coeficente de correlación (r) Pearson:
| r = | n·(∑X·Y) - (∑X)·(∑Y) |
| √[n·(∑X²) - (∑X)²]·[n·(∑Y²) - (∑Y)²] |
Modelos de Regresión
Un modelo de regresión, es una manera de expresar dos ingredientes esenciales de una relación estadística:
- Una tendencia de la variable dependiente Y a variar conjuntamente con la variación de la o las X de una manera sistemática
- Una dispersión de las observaciones alrededor de la curva de relación estadística
Estas dos características están implícitas en un modelo de regresión, postulando que:
- En la población de observaciones asociadas con el proceso que fue muestreado, hay una distribución de probabilidades de Y para cada nivel de X
- Las medias de estas distribuciones varían de manera sistemática al variar X
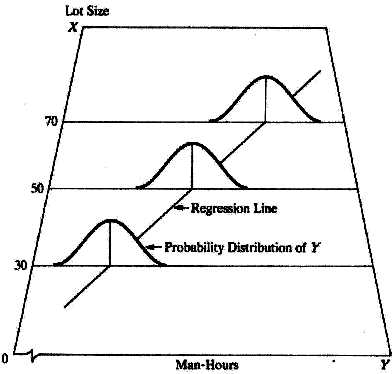
Representación gráfica del modelo de regresión lineal
• Nota: en esta figura se muestran las distribuciones de probabilidades de Y para distintos valores de X
Autor: Olga Susana Filippini. Argentina.
Editor: Ricardo Santiago Netto (Administrador de Fisicanet).
- ‹ Anterior
- |
- Siguiente ›
Coeficiente de correlación lineal. Modelos de Regresión. ¿Qué es la correlación y regresión?