Inferencia estadística (segunda parte)
Estimadores puntuales y por intervalo de confianza para media y varianza poblacionales
Métodos de estimación
Hay varios métodos de estimación, el de máxima verosimilitud es el que proporciona estimadores consistentes pero no siempre insesgados. Los estimadores mencionados en los puntos anteriores (x, S²) eran estimadores máximo verosimiles. El mismo resultado se puede obtener por el método de los momentos.
El método de mínimos cuadrados se verá cuando se trate regresión.
Estimación por intervalos
Dada una muestra aleatoria X₁, X₂, …, Xₙ, de una población con función de densidad f(x;θ) Un intervalo de confianza, de extremos Linferior y Lsuperior, para el parámetro θ de la población es un par ordenado de funciones reales de las n medidas de la muestra.
I·θ = [Linferior (X₁, …, Xₙ); Lsuperior (X₁, …, Xₙ)]
Construidas de forma que la probabilidad de que los extremos contengan al verdadero valor del parámetro es un valor prefijado (1 - α). Al número (1 - α) se le denomina "nivel de confianza".
- El nivel de confianza suele ser 0,95 (95%) ó 0,99 (99%). La interpretación práctica es sencilla, por ejemplo si el nivel de confianza es del 95%, significa que en el 95% de las veces que repitiéramos el experimento, el intervalo de confianza calculado contendría al verdadero valor del parámetro y en el 5% restante el intervalo no contendría el verdadero valor
- Una vez que el intervalo de confianza ha sido calculado para una muestra concreta, el intervalo obtenido contiene o no contiene al verdadero valor del parámetro, con probabilidad 1, por esa razón, cuando ya tenemos un valor concreto hablamos de confianza y no de probabilidad. Confiamos en que el intervalo que hemos calculado sea del 95% que contiene el verdadero valor
Nivel de confianza gráficamente
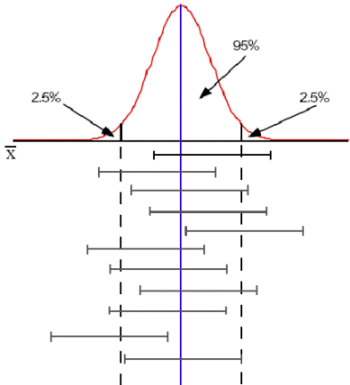
Figura 2: interpretación del nivel de confianza en un intervalo para la media de una distribución normal.
Intervalo de confianza para la media poblacional, σ conocido
Supongamos que disponemos de una población en la que tenemos una variable aleatoria con distribución N(μ, σ) con σ conocida (de estudios previos, por ejemplo).
Obtenemos una muestra de tamaño n y deseamos estimar la media μ de la población. El estimador puntual de la misma es la media muestral cuya distribución muestral es conocida la cantidad
x ≡ N(μ, σ/√n)
z = (x - μ)/(σ/√n)
Tendrá distribución normal estándar
Sobre la distribución N(0, 1) podremos seleccionar dos puntos simétricos -zα/2 y zα/2, tales que
P(-zα/2 ≤ Z ≤ zα/2) = 1 - α
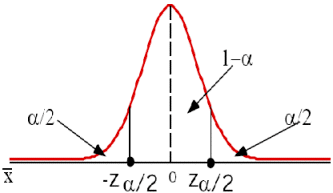
Figura 1: selección de los puntos críticos para el cálculo del intervalo de confianza.
Sustituyendo Z por su valor en este caso particular
| P{-zα/2 ≤ | x - μ | ≤zα/2} = 1 - α |
| σ | ||
| √n |
Despejando nos queda el intervalo de confianza,
| P{x - zα/2 | σ | ≤ μ ≤ x + zα/2 | σ | } = 1 - α |
| √n | √n |
Ejemplo:
Obtener un intervalo de confianza del 95 % para el promedio de un lote de 500 novillos, de los cuales se pesa una muestra de 25 animales, obteniéndose un = 390 kg. Se sabe que σ² es de 400 kg²
| {390 - 1,96 | 20 | ≤ μ ≤ 390 + 1,96 | 20 | } |
| √25 | √25 |
{382,16 ≤ μ ≤ 397,84}
Recordemos que si la varianza poblacional es desconocida y la variable es normal o se puede aproximar a la distribución normal por el Teorema central del límite, entonces se usaría la t de Student con n - 1 grados de libertad y el desvío estándar muestral.
El intervalo de confianza que resulta,
| P{x - t(α/2;n - 1) | s | ≤ μ ≤ x + t(α/2;n - 1) | s | } = 1 - α |
| √n | √n |
Ejemplo:
En un establecimiento dedicado a la elaboración de alimentos balanceados para aves, se afirma que su producto aumenta el peso promedio de las aves en 30 g diarios. En una muestra de 9 aves tomadas al azar, se obtuvo un aumento promedio de 35 g con desviación de 3,04 g. Estimar el intervalo de confianza del 95 % para el verdadero aumento promedio
| {35 - 2,306 | 3,04 | ≤ μ ≤ 35 + 2,306 | 3,04 | } |
| √9 | √9 |
{32,66 ≤ μ ≤ 37,34}
Determinación del tamaño de muestra n para un grado de precisión dado
z1 - α/2·(σ/√n) es la mitad del ancho del intervalo de confianza (producto del coeficiente y el error estándar) y se denomina error máximo de estimación E.
Dado un valor de error y un cierto nivel de confianza, puedo estimar cuál sería el tamaño de la muestra.
Z²1 - α·σ²/E² = n
Intervalo de confianza para la varianza poblacional
Sea X una variable aleatoria con distribución normal con μ y σ desconocidos y sea X₁, X₂, …, Xₙ una muestra aleatoria de tamaño n.
El intervalo de confianza se construye a partir de la variable:
χ² = (n - 1)·S²/σ²
Que tiene una distribución ji-cuadrado con n - 1 grados de libertad y dos valores tales que delimiten el 100(1 - α)%
Pr {χ²(n - 1);α/2 ≤ χ²₍ₙ ₋ ¹₎ ≤ χ²(n - 1);α/2}
Reemplazando la variable χ² en el intervalo:
| Pr {χ²(n - 1);α/2 ≤ | (n - 1)·S² | ≤ χ²(n - 1);α/2} |
| σ² |
Despejando el intervalo de confianza queda,
| Pr{ | (n - 1)·S² | ≤ σ² ≤ | (n - 1)·S² | } = 1 - α |
| x²(n - 1);1-α/2 | x²(n - 1);α/2 |
Ejemplo:
Se sembró cierta variedad de trigo en parcela de cierta localidad, se extrajo una muestra al azar de 20 parcelas y se midió el rendimiento. Se obtuvo un rendimiento de 58 kilogramos por parcela y una desviación típica de 8 kg por parcela. Estimar la varianza poblacional con un nivel de confianza del 95 %, sabiendo que el rendimiento se distribuye normalmente
{(19)·64/32,9 ≤ σ² ≤ (19)·64/8,91}
{32,66 ≤ σ² ≤ 37,34}
Autor: Olga Susana Filippini. Argentina.
Editor: Ricardo Santiago Netto (Administrador de Fisicanet).
- ‹ Anterior
- |
- Siguiente ›