Inferencia estadística (primera parte)
Estimadores puntuales y por intervalo de confianza para media y varianza poblacionales
Introducción al tema
• El único método científico para validar conclusiones sobre un grupo de individuos a partir de la información que nos proporciona un subconjunto más o menos amplio de los mismos es el Método Estadístico
• En el experimento típico, el objetivo básico es estimar algunas características que describan la población de interés. Es decir:
▫ Estimar los parámetros que caracterizan a la función de probabilidad de la variable aleatoria en estudio
Mapa conceptual
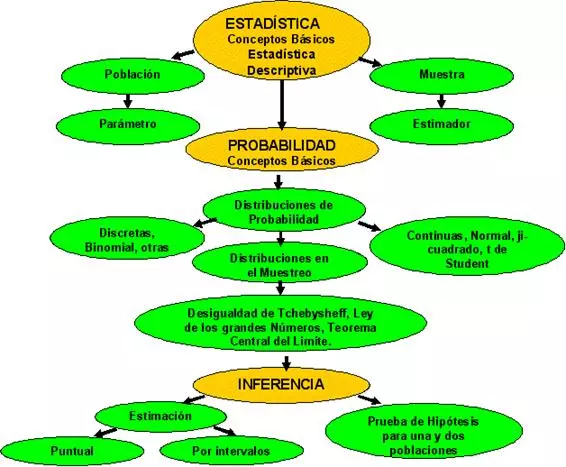
Mapa conceptual
Veamos el caso de un especialista en producción animal:
Después de alimentar un lote de terneros con una ración alimenticia particular, necesita expresar numéricamente el aumento medio de peso de sus animales
En este caso, suponemos que se dispone de los conocimiento suficientes como para decir:
La variable aleatoria x de nuestro problema, tiene una función de probabilidad conocida: f(X; θ1; θ2; …; θp) y depende de:
Parámetros θ1 hasta θp que son desconocidos.
Podría ocurrir que el aumento de peso de los terneros siguieran una distribución normal con media μ y varianza σ²
En este caso el experimentador persigue como objetivo, estimar a μ y σ²
Lo hará a partir de la manipulación de un conjunto de observaciones que ha de seleccionar de la población y que constituirán una muestra aleatoria de la misma.
Razonamiento a seguir:
- Pensar como se define la población y la muestra
- Qué tipo de procedimiento utilizar para seleccionar una muestra aleatoria
- Qué debería calcular para estimar los parámetros de interés. (estadístico)
- Qué función de distribución presentan los estimadores elegidos
- Cómo validar las estimaciones a partir de la muestra
Es decir inferir de la muestra a la población
Inferencia Estadística
La inferencia estadística es la forma de tomar decisiones basadas en probabilidades y presenta dos aspectos:
| 1. Estimación de parámetros: |
|
| 2. Prueba de Hipótesis con respecto a una función elegida como modelo | |
En esta clase discutiremos estos puntos
Estimación Puntual
- Una estimación puntual del valor de un parámetro poblacional desconocido (como puede ser la media, μ, o la desviación estándar, σ), es un número que se utiliza para aproximar el verdadero valor de dicho parámetro poblacional
- Una estimación puntual es el valor de la estadística de la muestra correspondiente
Estimadores puntuales de los parámetros de una población normal
Sea una muestra aleatoria simple, X1, X2, ……, Xn de una población con distribución N(μ, σ²).
-Estimador de la media
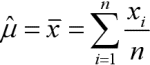
La distribución muestral de la media es:
x ≡ N(μ, σ/√n)
Estimadores puntuales de los parámetros de una población normal
S/√n estima a la desviación típica de la media σ/√n y se denomina error estándar de la media muestral, por esta razón se dice que el error estándar de la media mide la variabilidad de la media en el muestreo.
-Estimador de la Varianza
Varianza muestral
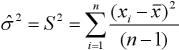
Sea X1, X2, …, Xn, una muestra aleatoria simple de una población X ≡ N(μ, σ²), entonces la variable aleatoria.
| n ∑ i = 1 | (xi - x) |
| σ² | |
Sigue una ji-cuadrado con n - 1 grados de libertad.
Del resultado anterior se deduce que la variable (n - 1)·S²/σ² sigue una distribución ji-cuadrado con n - 1 grados de libertad.
Realizada la estimación de un parámetro cabe preguntarse:
1) ¿Es exacta la estimación?
2) ¿Es probable que la estimación sea alta o baja?
3) ¿Con otra muestra se obtendría el mismo resultado, o bastante diferente?
4) La calidad de un procedimiento de estimación ¿mejora bastante si la estadística de la muestra es menos variable e insesgada a la vez?
Estimadores y propiedades deseables de los estimadores
La distancia entre el estimador y el parámetro a estimar puede medirse mediante los que se denomina el error cuadrático medio, que se define como el valor esperado del cuadrado de la diferencia entre el estimador y el verdadero parámetro.
ECM (Θ) = E(Θ - θ)²
El ECM es importante ya que puede escribirse como
ECM (Θ) = AVR (Θ) + [θ - E(Θ)]²
Una es la varianza del estimador y otra el cuadrado del sesgo.
Ausencia de sesgo
Se dice que un estimador es insesgado (o centrado) si la esperanza del estimador coincide con el parámetro a estimar E(Θ) = θ.
Consistencia
Se dice que un estimador es consistente si se aproxima cada vez más al verdadero valor del parámetro a medida que se aumenta el tamaño muestral.
Pr[(Θ - θ) > ε] ⟶ 0
n ⟶ ∞, ε > 0
La distribución del estimador se concentra más alrededor del verdadero parámetro cuando el tamaño muestral aumenta.
Eficiencia
Es claro que un estimador será tanto mejor cuanto menor sea su varianza, ya que se concentra más alrededor del verdadero valor del parámetro. Se dice que un estimador insesgado es eficiente si tiene varianza mínima.
Suficiencia
Un estimador es suficiente si utiliza una cantidad de la información contenida en la muestra de manera que ningún otro estimador podría extraer información adicional de la muestra sobre el parámetro de la población que se está estimando.
Efectos de la variabilidad y el sesgo
| Sesgo negativo (subestimación) | Insesgada (estimación en el blanco) | Sesgo positivo (sobreestimación) | |
| Alta variación | |||
| Baja variación |
Autor: Olga Susana Filippini. Argentina.
Editor: Ricardo Santiago Netto (Administrador de Fisicanet)
- ‹ Anterior
- |
- Siguiente ›