Superficie de nivel y curvas en ℜ³ (primera parte)
Conjuntos:
Abierto: Es aquel que no incluye la frontera (todos los puntos son interiores).
Cerrado: Es aquel que incluye toda su frontera.
Acotado: ℜ es acotado si ∃ k > 0 / ℜ ⊂ E(0, k)
Compacto: cerrado y acotado.
Conexo: Cuando dados 2 puntos cualesquiera del conjunto, se los puede unir con una curva que este incluida en el conjunto.
Convexo: Cuando dados 2 puntos cualesquiera del conjunto, el segmento que los une esta incluido en el conjunto.
Si es convexo:
![]()
No es convexo:
Funciones:
F:A ⊂ ℜᵐ ⟶, m > 1 campo vectorial
F:A ⊂ ℜⁿ ⟶ ℜ, m = 1 campos o funciones escalares
Conjunto de nivel (para campos escalares):
Definición:
Dada F:A ⊂ ℜⁿ ⟶ ℜ y k ⊂ ℜ, se llama conjunto de nivel k de F al conjunto de puntos de A tal que F(x) = k
Para f:A ⊂ ℜ² ⟶ ℜ: F(x, y) = k = > curva de nivel
Para f:A ⊂ ℜ³ ⟶ ℜ: F(x, y, z) = k = > superficie de nivel
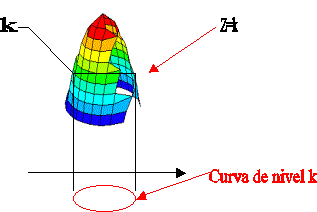
Interpretación geométrica: El conjunto de nivel k de una función de 2 variables x e y es la sombra o la proyección de la curva que resulta de intersectar el gráfico de la función con el plano z = k.
Superficie de nivel:
F(x, y, z) = k
Ejemplo nº 1
3·x - 2·y + z = k
Para k = 1:
3·x - 2·y + z = 1 ⟶ (x, y, z)·(3, -2, 1) = k ⇒ Fijo
Para k = -2:
3·x - 2·y + z = -2 ⟶ (x - a)·v = 0 ⇒ x·v = a·v ⇒ Fijo
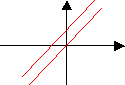
⇒ Si varío k, varío el origen del plano (lo desplazo)
A medida que varío k me van quedando planos paralelos.
Ejemplo nº 2
F(x, y) = y - 2·x, x ⊂ ℜ²
Planteo F(x, y) = k, k ⊂ ℜ ⇒ y - 2·x = k ⇒ y = 2·x + k
F(x, y, z) = z - x² - y² - 4
Planteo F(x, y, z) = k ⇒ z - x² - y² - 4 = k ⇒ z = x² + y² + 4 + k
Parametrizaciones: Curvas en ℜ²
a)
F(x) = x², x ⊂ [-1, 4]
Ecuación cartesiana del gráfico de F:
y = F(x) ⇒ Y = x², -1 ≤ x ≤ 4
Ecuación vectorial del gráfico de F:
x = (t, t²), t ⊂ [-1, 4]
Ecuaciones paramétricas del gráfico de F:
x = t ∧ y = t², t ⊂ [-1, 4]
La función g:[-1, 4] ⟶ ℜ² se denomina parametrización del gráfico de F y está definida por: g(t) = (t, t²), t ⊂ [-1, 4]
b)
F(x) = 2·x + 1, x ⊂ ℜ ecuación cartesiana y = 2·x + 1, x ⊂ ℜ.
Parametrización: intento x = t ⇒ y = 2·t + 1} g(t) = (t, 2·t + 1), t ⊂ ℜ
X = (t, 2·t + a), t ⊂ ℜ ecuación vectorial.
Parametrización de una circunferencia:
x² + y² = R²
EP: x = R·cos t, t ⊂ [0, 2·π]
y = R·sen t
EV: x = (R·cos t, R·sen t), t ⊂ [0, 2·π]
G = (R·cos t, R·sen t), t ⊂ [0, 2·π]
Observación:
Para recorrer las curvas de manera inversa a la normal: de [a, b] pasa a [-b, -a]
Curva
Definición:
Dada una función g:[a, b] ⊂ ℜ ⟶ ℜⁿ, contínua, se llama curva al conjunto imagen de g
Curva no completa = arco de curva.
Curvas en ℜ³
| Z + y = 3 | EP: x = t |
| Y = x² | y = t² |
| Z = 3 - t² |
EVG(t) = (t, t², 3 - t²), t ⊂ ℜ
Superficie
Definición:
Dada una función g: A ⊂ ℜ² ⟶ ℜⁿ, contínua, se llama superficie al conjunto imagen de g.
Límites
Propiedades:
Si:
| lim x ⟶ a | F(x) = b ∧ | lim x ⟶ a | g(y) = L |
| lim x ⟶ a | (g o F)(x) = L |
Si:
| lim x ⟶ a | F(x) = L |
| lim x ⟶ a | Fᵢ(x) = Lᵢ |
1 ≤ i ≤ m; (se acercan las componentes).
Límites por curvas:
| Si ∄ el límite para alguna curva parametrizada por "g" tal que g(t₀) = A ⇒ ∄ | lim x ⟶ a | F(x) |
Ejemplo nº 3
| lim (x, y) ⟶ (1, 1) | x - y - 2 |
| x - 1 |
| Tomo y = 1 ⇒ | lim x ⟶ 1 | x - 1 | = 1 |
| x - 1 |
| Tomo x = 1 ⇒ | lim y ⟶ 1 | y - 1 | = -1 |
| 1 - y |
| Luego, ∄ | lim (x, y) ⟶ (1, 1) | F(x, y) = 1 |
Observación: La curva que propongo, debe pasar por el punto de trabajo del limite.
Recordar:
| |x| ≤ |x| ⇒ x² ≤ x² + y² ⇒ | x² | ≤ 1 |
| x² + y² |
Continuidad
F contínua en x₀ y G contínua en F(x₀) ⇒ (G₀F) contínua en x₀
F contínua en x₀ < = > Fᵢ contínua en x₀, 1 ≤ i ≤ m
Tipos de discontinuidad:
Esencial:
| Cuando ∄ | lim x ⟶ x₀ | F(x) |
Evitable:
Cuando existe el límite pero no F(x₀) o bien ∃ F(x₀) pero lim ≠ F(x₀)
Derivabilidad
Definición:
Derivada direccional:
Dada F:A ⊂ ℜⁿ ⟶ ℜᵐ, x₀ y ř ⊂ ℜⁿ, se define la derivada direccional de F en x₀ según el versor ř como:
| F'(x₀, γ) = | lim h ⟶ 0 | F(x₀ + h·γ) - F(x₀) | = | ∂F(x₀) |
| h | ∂γ |
Propiedades:
Principio de homogeneidad:
F'(x₀, λ ř) = λ F'(x₀, ř), λ ≠ 0, λ ⊂ ℜ
Propiedad 2:
Si existe la derivada direccional en un punto, existen las derivadas de las componentes y viceversa.
Derivadas parciales:
Caso especial de direccionales. Una derivada parcial es una direccional respecto de un versor de la base canónica.
Regla práctica de calculo:
F(x, y) = ln (x² + y²)
F'ₓ(x, y) = 2·x/(x² + y²)
F'y(x, y) = 2·y/(x² + y²)
Dom (F'ₓ) I Dom (F)

Observación:
La derivada de un vector es la derivada de las componentes.
Interpretación geométrica:
Válida para F:A ⊂ ℜ² ⟶ ℜ
| F'(x₀, y₀) = | lim h ⟶ 0 | F(x₀ + h, y₀) - F(x₀, y₀) |
| h |
| F'(x₀, y₀) = | tg α |
Teorema del valor medio:
a)
Dada F:[a, b] ⟶ ℜ, contínua en [a, b] y derivable en (a, b), entonces existe c ⊂ (a, b) tal que:
F(b) - F(a) = F'(c)·(b - a)
b)
Dada F:A ⊂ ℜⁿ ⟶ ℜ, A abierto y convexo, F ⊂ C¹, a ⊂ A y b ⊂ A, entonces:
F(b) - F(a) = F'(c, b - a) = F'(c, ř) |b - a|, γ = (b - a)/|b - a|, c ⊂ segmento a b, c ≠ a y c ≠ b

Aplicaciones a curvas:
Definición:
Punto regular:
Dada C curva de ℜⁿ, de ecuación vectorial x = g(t) t ⊂ A, se dice que A ⊂ C, A = g(t₀), es un punto regular de C si:
a) ∃ g'(t₀) y
b) g'(t₀) ≠ 0
Observaciones:
a) Si un punto no es regular se lo llama singular
b) Si una curva tiene todos los puntos regulares ⇒ es regular
Autor: Marcelo Ariel Jusid.
Editor: Ricardo Santiago Netto (Administrador de Fisicanet).
- ‹ Anterior
- |
- Siguiente ›