Límites en varias variables
Definición:
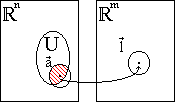
Sea f: U ⊂ ℜⁿ ⟶ ℜᵐ y ā un punto de acumulación de U. Entonces se dice que:
| lim x ⟶ a | f(X) = l ∈ ℜᵐ |
Si:
∀ ε > 0, ∃ δ > 0 / x ∈ U, 0 < d(x, ā) < δ ⟶ d(f(x), f) < ε
Gráficamente podemos verlo así: Siempre existe un Δ tal que las imágenes de la parte de la bola de centro ā y radio Δ que pertenece a U pertenecen a una bola de radio ε con centro en f.
Ejemplo nº 1
Demostrar que:
| lim (x, y) ⟶ (0, 0) | 4·x²·(y + 1) + 2·y² | = 2 |
| 2·x² + y² |
d(f(x, y), 2) < ε ⇔ d((x, y)(0, 0)) < δ
d(f(x, y), 2) = |f(x, y) - 2| =
| = | 4·x²·(y + 1) + 2·y² | - 2 | = |
| 2·x² + y² |
| = | 4·x²·(y + 1) + 2·y² - 4·x² - 2·y² | - 2 | = |
| 2·x² + y² |
| = | 4·x²·(y + 1) + 2·y² - 4·x² - 2·y² | = |
| 2·x² + y² |
| = | 4·x²·y + 4·x² + 2·y² - 4·x² - 2·y² | = |
| 2·x² + y² |
| = | 4·x²·y | = |
| 2·x² + y² |
| = | 4·x²·|y| | ≤ | 4·x²·|y| | = 2·|y| |
| 2·x² + y² | 2·x² |
Como:
(x² + y²)½ < δ ⇒ |y| ≤ δ
d(f(x, y), 2) ≤ 2·|y| ≤ 2·δ
δ = ε/2
Con lo que queda comprobado.
Definición:
Decimos que el límite de f(x) es infinito si:
| lim x ⟶ a | f(X) = ∞ ⇔ ∀ K > 0 ∃ δ > 0/x ∈ U, (0 < (d(x,ā)) < δ) ⟶ d(f(x),0) > K |
Es decir, si por mucho que nos acerquemos a ā, la distancia de la función al cero es muy grande.
Definición:
Si E ⊂ ℜⁿ es un contorno de ā ∈ ℜⁿ es, llamamos entorno perforado de ā a E - {ā} Propiedades:
1. Si f(x) tiene límite en ā, este es único
2. Si f(x),g(x): ℜⁿ ⟶ ℜᵐ tienen límites f₁, f₂ en ā respectivamente, entonces:
| lim x ⟶ a | [f(x) ± g(x)] = l₁ ± l₂ |
3. Si f(x),g(x): ℜⁿ ⟶ ℜᵐ tienen límites f₁, f₂ en ā respectivamente, entonces:
| lim x ⟶ a | [f(x)·g(x)] = l₁·l₂ |
4. Si además g(x) ≠ 0 en un entorno perforado de ā y l₂ ≠ 0, entonces:
| lim x ⟶ a | [f(x)/g(x)] = l₁/l₂ |
Observación:
El principal problema que nos encontramos a al hora de calcular límites es como acercarnos al punto. Hay muchas maneras (por rectas, parábolas, cúbicas, etc). Pero como el límite ha de ser siempre el mismo, podemos asegurar que no existe si el límite nos da diferente para varios modos de acercarse. El caso más sencillo a probar es acercarse al origen por una recta de pendiente m.
Ejemplo nº 2
| lim (x, y) ⟶ (0, 0) | x·y + y³ |
| x² - y² |
Nos acercamos por una trayectoria recta:
y = m·x
| lim x ⟶ 0 | x·(m·x) + (m·x)³ |
| x² - (m·x)² |
| lim x ⟶ 0 | m·x² + m³·x³ |
| x² - m²·x² |
| lim x ⟶ 0 | (m + m³·x)·x² |
| (1 - m²)·x² |
| lim x ⟶ 0 | m + m³·x | = | m |
| 1 - m² | 1 - m² |
El límite depende de la pendiente, luego el límite no existe.
Sin embargo, el hecho de que por un tipo de trayectorias el límite sea el mismo no indica que el límite exista; solo dice que si existiera debería ser ese.
Ejemplo nº 3
| lim (x, y) ⟶ (0, 0) | x³ |
| x² - y |
| lim x ⟶ 0 | x³ |
| x² - (m·x) |
| lim x ⟶ 0 | x³ |
| x·(x - m) |
| lim x ⟶ 0 | x² | = 0 ∀ m ∈ ℜ |
| x - m |
Si f(x) tuviera límite, debería ser cero. Si probamos ahora con otro tipo de trayectorias, como por ejemplo:
y = x² - x³
| lim (x, y) ⟶ (0, 0) | x³ |
| x² - y |
| lim x ⟶ 0 | x³ | = 1 |
| x² - x² + x³ |
Luego el límite no existe.
Autor: José Luis Martínez-Avila. España.
Editor: Ricardo Santiago Netto (Administrador de Fisicanet).
- ‹ Anterior
- |
- Siguiente ›