Problema nº 2 de números complejos o imaginarios, ecuaciones - TP04
Enunciado del ejercicio nº 2
Obtener los valores naturales de "x" que satisfagan:
| x·(x - i) + (x + 0,8)·i + 8·x - 8,6 = | -(1 - i)² |
| 2 + i |
Solución
En el primer miembro aplicamos distributiva del producto respecto a la suma y a la resta, en el segundo miembro resolvemos el binomio al cuadrado:
| x·x - x·i + x·i + 0,8·i + 8·x - 8,6 = | -(1² - 2·1·i + i²) |
| 2 + i |
Como i² = -1:
| x² + 0,8·i + 8·x - 8,6 = | -[1 - 2·i + (-1)] |
| 2 + i |
En el segundo miembro multiplicamos y dividimos por el conjugado del denominador:
| x² + 8·x - 8,6 + 0,8·i = | -(1 - 2·i - 1)·(2 - i) |
| (2 + i)·(2 - i) |
| x² + 8·x - 8,6 + 0,8·i = | -(-2·i)·(2 - i) |
| 2² - i² |
| x² + 8·x - 8,6 + 0,8·i = | 2·i·(2 - i) |
| 4 - (-1) |
| x² + 8·x - 8,6 + 0,8·i = | 2·i·2 - 2·i·i |
| 4 + 1 |
| x² + 8·x - 8,6 + 0,8·i = | 4·i - 2·i² |
| 5 |
| x² + 8·x - 8,6 + 0,8·i = | 4·i - 2·(-1) |
| 5 |
| x² + 8·x - 8,6 + 0,8·i = | 4·i + 2 |
| 5 |
5·x² + 5·8·x - 5·8,6 + 5·0,8·i = 4·i + 2
5·x² + 40·x - 43 + 4·i = 4·i + 2
Igualamos a cero:
5·x² + 40·x - 43 - 2 + 4·i - 4·i = 0
Nos queda una ecuación de segundo grado, resolvemos aplicando la ecuación cuadrática (Báscara o Bhaskara) que dará dos resultados:
5·x² + 40·x - 45 = 0
| x1,2 = | -40 ± √40² - 4·5·(-45) |
| 2·5 |
Resolvemos:
| x1,2 = | -40 ± √1.600 + 900 |
| 10 |
| x1,2 = | -40 ± √2.500 |
| 10 |
| x1,2 = | -40 ± 50 |
| 10 |
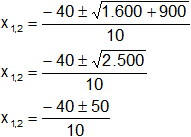
x1,2 = -4 ± 5
x₁ = -4 + 5
x₂ = -4 - 5
Resultado, los valores de "x" que satisfacen la igualdad son:
x₁ = 1
x₂ = -9
Verificar.
Resolvió: Ricardo Santiago Netto. Argentina
- ‹ Anterior |
- Regresar a la guía TP04
- | Siguiente ›
Ejemplo, resolver ecuaciones con números complejos