Problema nº 3 de operaciones con números reales, racionalización - TP13
Resolver los siguientes ejercicios
Problema nº 3
a)
Solución
Racionalizamos el denominador:
| = | 7 - √5 | · | 3 - √5 | = |
| 3 + √5 | 3 - √5 |
| = | (7 - √5)·(3 - √5) | = |
| (3 + √5)·(3 - √5) |
Aplicamos diferencia de cuadrados en el denominador y distributiva del producto con respecto a la resta en el numerador:
| = | 3·7 - √5·7 + [3·(-√5) - √5·(-√5)] | = |
| 3² - (√5)² |
| = | 21 - 7·√5 + [-3·√5 + (√5)²] | = |
| 9 - 5 |
| = | 21 - 7·√5 + (-3·√5 + 5) | = |
| 4 |
Extraemos factor común "2" en el numerador:
Simplificamos y expresamos el resultado:
b)
Solución
Racionalizamos el denominador aplicando diferencia de cuadrados:
| = | √6·(2 + √6) | = |
| (2 - √6)·(2 + √6) |
Aplicamos distributiva del producto con respecto a la resta en el numerador:
Extraemos factor común "-2" en el numerador:
Simplificamos y expresamos el resultado:
c)
Solución
Racionalizamos el denominador aplicando diferencia de cuadrados. En este caso sólo invertimos un signo a la vez:
| 2 | · | (√2 + √3) - √5 | = |
| (√2 + √3) + √5 | (√2 + √3) - √5 |
| = | 2·(√2 + √3 - √5) | = |
| (√2 + √3)² - (√5)² |
En el denominador resolvemos el binomio al cuadrado:
| = | 2·(√2 + √3 - √5) | = |
| (√2)² + 2·√2·√3 + (√3)² - 5 |
| = | 2·(√2 + √3 - √5) | = |
| 2 + 2·√6 + 3 - 5 |
Simplificamos:
Racionalizamos nuevamente el denominador:
Resolvemos y expresamos el resultado:
| 2 | = | (√2 + √3 - √5)·√6 |
| √2 + √3 + √5 | 6 |
d)
Solución
Racionalizamos el denominador aplicando diferencia de cuadrados, invertimos el signo de una de las raíces:
| = | 12 | · | (3 + √5) + 2·√2 | = |
| (3 + √5) - 2·√2 | (3 + √5) + 2·√2 |
| = | 12·(3 + √5 + 2·√2) | = |
| (3 + √5)² - (2·√2)² |
En el denominador resolvemos el binomio al cuadrado:
| = | 12·(3 + √5 + 2·√2) | = |
| 3² + 2·3·√5 + (√5)² - 4·2 |
| = | 12·(3 + √5 + 2·√2) | = |
| 9 + 6·√5 + 5 - 8 |
| = | 12·(3 + √5 + 2·√2) | = |
| 6 + 6·√5 |
Extraemos factor común "6" en el denominador:
| = | 12·(3 + √5 + 2·√2) | = |
| 6·(1 + √5) |
Simplificamos:
| = | 2·(3 + √5 + 2·√2) | = |
| 1 + √5 |
Racionalizamos nuevamente el denominador:
| = | 2·(3 + √5 + 2·√2) | · | 1 - √5 | = |
| 1 + √5 | 1 - √5 |
| = | 2·(3 + √5 + 2·√2)·(1 - √5) | = |
| 1² - (√5)² |
| = | 2·(3 + √5 + 2·√2)·(1 - √5) | = |
| 1 - 5 |
| = | 2·(3 + √5 + 2·√2)·(1 - √5) | = |
| -4 |
Simplificamos:
| = | (3 + √5 + 2·√2)·(1 - √5) | = |
| -2 |
Aplicamos distributiva del producto con respecto a la suma y a la resta en el numerador:
| = | 3 + √5 + 2·√2 - 3·√5 - (√5)² - 2·√2·√5 | = |
| -2 |
| = | 3 + √5 + 2·√2 - 3·√5 - 5 - 2·√10 | = |
| -2 |
| = | 2·√2 - 2·√5 - 2 - 2·√10 | = |
| -2 |
Extraemos factor común "-2" en el numerador:
| = | -2·(-√2 + √5 + 1 + √10) | = |
| -2 |
Simplificamos:
= -√2 + √5 + 1 + √10
Expresamos el resultado:
| 12 | = -√2 + √5 + 1 + √10 |
| 3 + √5 - 2·√2 |
e)
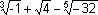 =
=
Solución
Resolvemos las raíces:
= -1 + 2 - (-2) =
= -1 + 2 + 2
Expresamos el resultado:
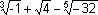 = 3
= 3
Resolvió: Ricardo Santiago Netto. Argentina
Ejemplo de operaciones con números reales, racionalización
![]() =
=![]() = 3
= 3