Guía nº 14-a de ejercicios de operaciones con números reales
• Raíz: se llama raíz de un número o de una expresión algebraica a todo número o expresión algebraica que elevada a una potencia n; reproduce la expresión dada.
Elementos de la raíz
| Indice | ← | ⁵√16·a²·m | ⟶ | Signo radical |
| ⟶ | Cantidad subradical o radicando | |||
- Radical: se llama radical a toda raíz indicada de una cantidad.
Si la raíz es exacta tenemos una cantidad racional.
Ejemplos:
√25; √4·a²; ∛27; ∛64·m³; etc.
Si la raíz es inexacta tenemos una cantidad irracional o radical propiamente dicha.
Ejemplos:
√2; √3·a; ∛15; ∛3·a²; etc.
El grado de un radical lo indica el índice de la raíz.
Extracción de factores fuera del radical
Pueden extraerse factores fuera del radical; cuando los factores de la cantidad sub-radical contiene un exponente igual o mayor que el índice del radical.
Ejercicio de aplicación:
Extraer todos los factores posibles de los siguientes radicales:
1) √18 =
2) 3·√48 =
3) ∛16 =
4) √9·a³ =
5) √50·a²·b =
6) √98·a³·b⁵·c⁷ =
7) 2·√75·x⁴·y⁵ =
8) 3·√81·x³·y⁴ =
9) ⅐·√49·x³·y⁷ =
10) ½·√108·a⁵·b⁷ =
11) ⅓·√27·a⁵·m⁷ =
12) ⅗·√125·m·n⁶ =
13) 2·a·√44·a³·b⁷·c⁹ =
14) 2·∛16·x²·y⁷ =
15) 4·∛250·a³·b⁸ =
16) ½·∛128 =
17) ⅔·∛27·m²·n⁸ =
18) 2·x·y·∛128·x²·y⁸ =
19) 5·a·∛160·x⁷·y⁹·z¹³ =
20) 2·∜243 =
21) ∜80·a⁴·b⁵·c¹² =
22) 3·∜5·x⁸·y¹⁴·z¹⁶ =
23) (3/2)·∜32·m·n⁸ =
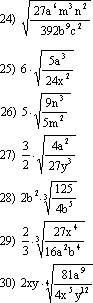
Introducción de factores dentro del radical
Está operación es inversa a la extracción de radicales. Para introducir factores dentro del radical; se eleva los factores de la cantidad situada fuera del signo radical a una potencia igual al índice de la raíz, está cantidad se escribe dentro del radical y se multiplica por la cantidad sub-radical si lo hubiera, y finalmente se efectúan las operaciones indicadas dentro del radical.
Ejercicio de aplicación:
Introducir dentro del radical todos los factores posibles que se encuentren fuera de él:
1) 3·√5 =
2) 2·√3 =
3) ½·√2 =
4) 2·√a =
5) 5·a·√b =
6) 3·a·√2·a² =
7) 3·a²·∛a²·b =
8) 5·x²·y·√3 =
9) a·b²·∛a²·b =
10) 4·m·∛2·m² =
11) 2·a·∜8·a·b³ =
12) 4·a·√2·x·y =
13) ½·∛8 =
14) 5·a²·∜a =
15) ⅒·a²m³∛a·x·m³ =
16) ½·a⁻²·b·∛4·a·b·x =
17) ⅒·a³·x²·b·∛1.000·a⁵·b·x³ =
18) a⁻⁵·x⁻¹·∛a³·x⁻² =
19) 3·n³·p·∜2·m =
20) 5·x·y⁵·√x³·y =
21) 20·a³·b²·∛2·b² =
22) 7·b²·∛3·a =
23) 5·m·n²·p³·√2·m³·n·p² =
24) 2·a²·b·c³·∛7·c =
Reducción de radicales al mínimo común índice
Está operación consiste en convertir radicales de distinto índice en radicales del mismo índice. Para eso, hallamos el m.c.m. de los índices que será el índice común; luego elevamos cada cantidad sub-radical a la potencia resultante de dividir el índice común con el índice de cada radical.
Ejemplos:
![]()
1°) Los índices son 2, 3 y 6. Hallamos el m.c.m. de los índices.
| 2 | 3 | 6 | 2 | |
| (1) | - | 3 | 3 | |
| (1) | (1) | El m.c.m. es 6 |
2°) Dividimos el índice común 6 con el índice de cada radical.
| 6 | 2 | 6 | 3 | 6 | 6 | ||
| (0) | 3 | (0) | 2 | (0) | 1 |
Luego, elevamos cada cantidad sub-radical a una potencia resultante de la división entre los índices.
![]()
3°) Efectuamos las operaciones indicadas dentro del radical.
![]()
Ejercicio de aplicación:
Reducir al mínimo común índice los siguientes radicales:
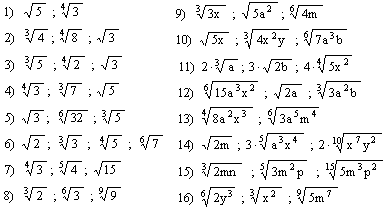
Radicales semejantes
Son aquellos radicales que tienen el mismo índice y la misma cantidad sub-radical; diferenciándose solamente en los signos y en los coeficientes.
Ejemplos:
½·√3; 5·√3; ⅜·√3; etc.
Suma y resta de radicales
Está operación se efectúa; primeramente extrayendo los factores de los radicales dados, luego verificamos si hay radicales semejantes y si los hay procedemos a sumarlo algebraicamente sus coeficientes acompañado del radical común y finalmente se escriben los radicales no semejantes con su propio signo si los hubiera.
Observación: Se recuerda que solamente se puede sumar o restar radicales, si dichos radicales son únicamente semejantes.
Ejercicio de aplicación:
Sumar los siguientes radicales indicados:
1) √45 - √27 - √20 =
2) √75 - √147 + √675 - √12 =
3) √175 + √243 - √63 - 2·√75 =
4) √80 - 2·√252 + 3·√405 - 3·√500 =
5) 2·√450 + 9·√12 - 7·√48 - 3·√98 =
6) 7·√450 - 4·√320 + 3·√80 - 5·√800 =
7) √20 + ⅓·√45 + 2·√125 =
8) ¼·√80 - ⅙·√63 - ⅑·√180 =
9) 5·√50 + (3/14)·√98 - ⅓·√162 =
10) 2·√45 - ¾·√125 - ½·√180 =
11) ½·√12 - ⅓·√18 + ¾·√48 + ⅙·√72 =
12) ¾·√176 - ⅔·√45 + ⅛·√320 + ⅕·√275 =
13) ⅐·√147 - ⅕·√700 + ⅒·√28 + ⅓·√2.187 =
14) ½·√3 - √27 + ⅓·√108 - ⅗·√300 =
15) ∛54 - ∛24 - ∛16 =
16) ∛875 + ∛448 + ∛189 =
17) ∛40 + ∛1.029 - ∛625=
18) 3·∛-24 - 4·∛-81 - ∛-375 =
19) 2·∛250 - 4·∛24 - 6·∛16 + ∛2.187 =
20) ∛81 - 3·∛375 + ∛686 + 2·∛648 =
21) 5·∛48 - 3·∛3.645 - 2·∛384 + 4·∛1.715 =
22) 4·∛-320 - 10·∛-40 - 2·∛-54 + 3·∛-1.024 =
23) 3·∛108 + ⅒·∛625 + ⅐·∛1.715 - 4·∛32 =
24) ½·∛24 - ⅔·∛54 + ⅗·∛375 - ¼·∛128 =
25) ⅗·∛625 - (3/2)·∛192 + ⅐·∛1.715 - ⅜·∛1.536 =
Autor: Hugo David Giménez Ayala. Paraguay.
Editor: Ricardo Santiago Netto (Administrador de Fisicanet).
- ‹ Anterior
- |
- Siguiente ›