Guía nº 14-b de ejercicios de operaciones con números reales
Multiplicación de radicales
a)
Para multiplicar radicales del mismo índice; se multiplican previamente los signos, luego los coeficientes entre sí y finalmente bajo un mismo radical común las cantidades sub-radicales entre sí. A continuación se efectúa las operaciones indicadas dentro del radical y se extraen los factores posibles fuera del radical si los hubiera.
Ejercicio de aplicación:
Multiplicar los siguientes radicales indicados:
1) √3·√6 =
2) 5·√12·3·√75 =
3) 2·√15·3·√10 =
4) 5·√21·2·√3 =
5) ½·√14·(2/7)·√21 =
6) 3·√6·√14·2·√35 =
7) ½·√21·⅔·√42·(3/7)·√22 =
8) ∛12·∛9 =
9) ⅚·∛15·12·∛50 =
10) ⅔·∛4·¾·∛6 =
11) 3·∛45·⅙·∛15·4·∛20 =
12) 3·√a·b·2·a·√b =
13) x·√2·a·½·√5·a =
14) 2·√a²·x·(3/2)·√a³ =
15) -⅓·x²·√5·m·n²·9·x·√2·m³·n²·(-√0,1·m²·n³) =
16) ½·√3·x·2·√⅓·x·3·√2·x·(-2)·√2·x =
17) ∛9·x²·y·∛81·x⁵ =
18) ¿·∛9·a²·y·8·∛3·a·b =
19) ⅔·∛x⁴·y³·¼·∛2·x·y⁴·∛4·x⁷·y⁶ =
20) -2·∛a·¿·∛a·x =
21) ∛(2·x⁴)/(25·y⁵)·∛(4·x⁵)/(5·y) =
![]()
b)
Para multiplicar radicales compuestos del mismo índice; se multiplican como el producto de 1 polinomio por 1 monomio o el producto de 2 polinomios.
Ejercicio de aplicación:
Multiplicar los siguientes radicales indicados:
1) (√2 - √3)·√2 =
2) (7·√5 + 5·√3)·2·√3 =
3) (2·√3 + √5 - 5·√2)·4·√15 =
4) (4 - √2)·(2 + 5·√2) =
5) (√2 - √3)·(√2 + 2·√3) =
6) (√5 + 2·√3)·(√5 - √3) =
7) (3·√7 - 2·√3)·(5·√3 + 4·√7) =
8) (√5 + 5·√3)·(2·√5 + 3·√3) =
9) (7·√5 - 11·√7)·(5·√5 - 8·√7) =
10) (3·√2 - 5·√3)·(4·√2 + √3) =
11) (√a + √b)·√a·b =
12) (12·√x + √y)·√x =
13) (√a - √2·a·b)·3·√a =
14) (4·√¼·y - ½·√x·y)·√x =
15) (√a - 2·√x)·(3·√a + √x) =
16) (∛27·a²·b + ∛125·a·b²)·⅓·∛a =
c)
Para multiplicar radicales compuestos de distinto índice; primeramente se reducen los radicales al mínimo común índice y luego se multiplican como si fueran radicales del mismo índice.
Ejercicio de aplicación:
Multiplicar los siguientes radicales indicados:
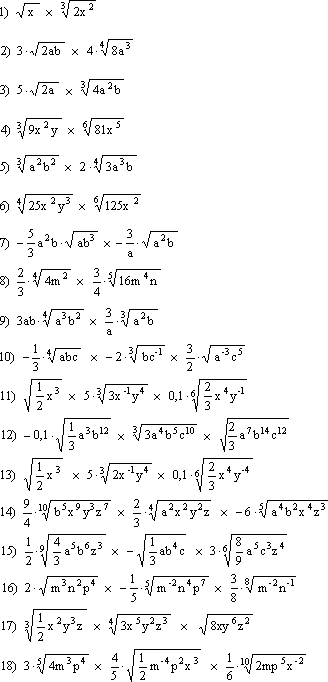
Autor: Hugo David Giménez Ayala. Paraguay.
Editor: Ricardo Santiago Netto (Administrador de Fisicanet).