Aplicaciones de los determinantes (segunda parte)
Discusión de los sistemas de ecuaciones lineales
Ejemplo de cálculo de las incógnitas en un sistema de ecuaciones lineales
Ejemplo nº 1
Discutir y calcular el valor de las incógnitas de los siguientes sistemas de ecuaciones lineales:
a)
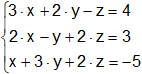
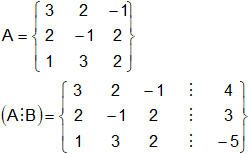
Calculamos a continuación el rango de A y el rango de la matriz ampliada (A ⋮ b):
El rango de la matriz A será:
= -3 - 4 = -7 ≠ 0
rango (A) ≥ 2
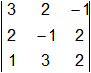= -6 + 4 - 6 - 1 - 8 - 18 = -35 ≠ 0
rango (A) = 3
El rango de la matriz ampliada (A ⋮ b):
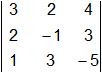= -15 + 6 + 24 + 4 - 20 - 27 = -28 ≠ 0
rango (A ⋮ b) = 3
Dado que rango (A) = rango (A ⋮ b) = 3 = número de incógnitas, el sistema es compatible y determinado; tiene, pues, una única solución. Resolvamos el sistema mediante la regla de Cramer:
Calculamos el det (A):
det (A) = 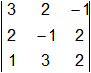= -6 + 4 - 6 - 1 - 8 - 18 = -35
Aplicando la regla de Cramer:
Polinomio característico
Consideremos una matriz n-cuadrada arbitraria:
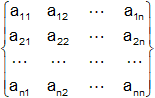
La matriz (A - λ·Iₙ), donde Iₙ es la matriz identidad n-cuadrada y λ un escalar indeterminado, se denomina matriz característica de A:
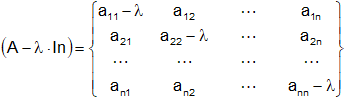
Su determinante, det (A - λ·Iₙ), que es un polinomio en λ, recibe el nombre de polinomio característico de A. Asimismo, llamamos a:
det (A - λ·Iₙ) = 0, ecuación característica de A.
Ejemplo nº 1
Hallar la matriz característica y el polinomio característico de la matriz A:
La matriz característica será (A - λ·Iₙ). Luego:
y el polinomio característico,
det (A - λ·Iₙ) = 
= (1 - λ)·(0 - λ) + 4
det (A - λ·Iₙ) = λ² - λ + 4
Así pues, el polinomio característico es λ² - λ + 4.
Valores propios y vectores propios
Sea A una matriz n-cuadrada sobre un cuerpo K. Un escalar λ ∈ Kⁿ se denomina un valor propio de A si existe un vector (columna) no nulo v ∈ Kⁿ para el que
Av = λ·v
Todo vector que satisfaga esta relación se llama vector propio de A perteneciente al valor propio λ. Los términos valor característico y vector característico (o autovalor y autovector) se utilizan con frecuencia en lugar de valor propio y vector propio.
Ejemplo nº 2
Sea:
y sean v₁ = (2, 3) y v₂ = (1, -1). Entonces:
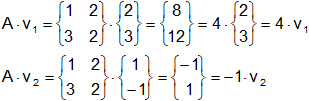
Así pues, v₁ y v₂ son vectores propios de A pertenecientes, respectivamente, a los valores propios λ₁ = 4 y λ₂ = -1 de A.
Autor: Jesús. España.
Editor: Ricardo Santiago Netto (Administrador de Fisicanet).
- ‹ Anterior
- |
- Siguiente ›