Aplicaciones de los determinantes (primera parte)
En el tema de matrices y su aplicación a los sistemas de ecuaciones lineales, se vio cómo resolverlas mediante el teorema de Gauss. Con los determinantes, y aplicando la regla de Cramer, veremos otra manera de calcular los sistemas de ecuaciones lineales.
Regla de Cramer
Los pasos a seguir para calcular los sistemas de ecuaciones según la regla de Cramer son los siguientes:
1) Hallar la matriz ampliada (A ⋮ b) asociada al sistema de ecuaciones, esto es: que la primera columna esté formada por las entradas de los coeficientes de la primera incógnita de las ecuaciones; que la segunda columna la formen las de la segunda incógnita, y así hasta llegar a la última columna, que estará constituida por las entradas de los términos independientes de las ecuaciones.
2) Calcular el determinante de A.
3) Aplicar la regla de Cramer, que consiste en:
a) Ir sustituyendo la primera columna del det (A) por los términos independientes;
b) Dividir el resultado de este determinante entre el det (A) para hallar el valor de la primera incógnita;
c) Continuar sustituyendo los términos independientes en las distintas columnas para hallar el resto de las incógnitas
Ejemplo:
Sea el sistema de ecuaciones lineales formado por dos ecuaciones con dos incógnitas:
3·x - 2·y = 1
x + 5·y = 3
Encontrar el valor de x e y mediante la regla de Cramer. Empezaremos con el primer paso, que consiste en hallar la matriz ampliada A ⋮ b asociada al sistema de ecuaciones lineales:
| x | y | b | ||||
| (A ⋮ b) = | 3 | -1 | ⋮ | 8 | ||
| 1 | 3 | ⋮ | 2 |
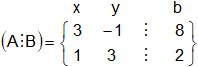
El segundo paso es calcular el determinante de A. Así pues:
| det A = | 3 | -2 | = 15 + 2 = 17 |
| 1 | 5 |
Y el tercero y último paso consiste en calcular las incógnitas:
| b | y | ||||||||
| 1 | -2 | ||||||||
| x = | 3 | -5 | = | 5 + 6 | = | 11 | |||
| 17 | 17 | 17 | |||||||
| x | b | ||||||||
| 3 | 1 | ||||||||
| y = | 1 | 3 | = | 9 - 1 | = | 8 | |||
| 17 | 17 | 17 | |||||||
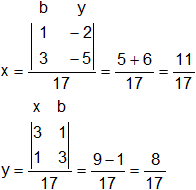
Discusión de los sistemas de ecuaciones lineales
A continuación, se estudiará la manera de saber de antemano si un sistema de ecuaciones lineales tienen o no solución y si tienen una única o infinitas soluciones. El estudio o discusión de los sistemas de ecuaciones se efectúa aplicando el teorema de Rouché-Fröbenius. Este dice que con un sistema de ecuaciones lineales pueden ocurrir dos cosas:
1) Que el sistema de ecuaciones sea un sistema compatible (S.C.), esto es, que tenga solución.
2) Que el sistema de ecuaciones sea un sistema incompatible (S.I.) o que no tenga solución.
El primer caso puede dividirse en dos:
a) Que sea un sistema compatible y determinado (S.C.D.), esto es, que tenga una única solución;
b) Que el sistema sea compatible e indeterminado (S.C.I.), es decir, que tenga infinitas soluciones.
Sea un sistema no homogéneo:
| a₁₁·x₁ + | … | + a₁ₙ·xₙ = b₁ | ||
| a₂₁·x₁ + | … | + a₂.ₙ·xₙ = b₂ | ||
| … | … | … | ||
| aₘ₁·x₁ + | … | + aₘₙ·xₙ = bₘ |
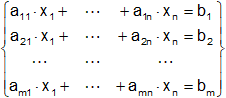
En consecuencia, la matriz ampliada Ab asociada al sistema de ecuaciones es:
| A ⋮ b = | a₁₁ | … | a₁ₙ | ⋮ | b₁ | ||
| a₂₁ | … | a₂.ₙ | ⋮ | b₂ | |||
| … | … | … | ⋮ | … | |||
| aₘ₁ | … | aₘₙ | ⋮ | bₘ |
y el sistema será compatible cuando:
rango (A) = rango (A ⋮ b), lo que suele expresarse diciendo que el rango de la matriz de coeficientes coincide con el rango de la matriz ampliada.
Si el sistema anterior es compatible y rango (A) = rango (A ⋮ b) = número de incógnitas, el sistema es compatible y determinado, es decir, tiene una única solución. Si, por el contrario, tenemos que rango (A) = rango (A ⋮ b) < número de incógnitas, el sistema es compatible e indeterminado, es decir, tiene infinitas soluciones.
Si rango (A) ≠ rango (A ⋮ b), el sistema es incompatible y no tiene ninguna solución.
Ejemplos:
Discutir, sin resolver, los siguientes sistemas de ecuaciones:
a)
x + 2·y = 5
2·x + 4·y = 13
b)
3·x - y = 8
x + 3·y = 2
c)
6·x - 2·y = -10
3·x - y = -5
a)
x + 2·y = 5
2·x + 4·y = 13
| A = | 1 | 2 | ||
| 2 | 4 |
| (A ⋮ I) = | 1 | 2 | ⋮ | 5 | ||
| 2 | 4 | ⋮ | 13 |
| rango (A) = | 1 | 2 | = 4 - 4 = 0 |
| 2 | 4 |
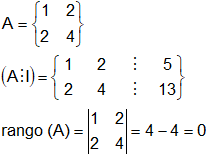
Rango (A) = 1
| rango (A ⋮ B) = | 1 | 5 | = 13 - 10 = 3 ≠ 0 |
| 2 | 13 |
Rango (A ⋮ B) = 2
Puesto que rango (A) = 1 ≠ rango (A ⋮ B) = 2, el sistema es incompatible; no existe ninguna solución.
b)
3·x - y = 8
x + 3·y = 2
| A = | 3 | -1 | ||
| 1 | 3 |
| (A ⋮ b) = | 3 | -1 | ⋮ | 8 | ||
| 1 | 3 | ⋮ | 2 |
| rango (A) = | 3 | -1 | = 9 + 1 = 10 ≠ 0 |
| 1 | 3 |
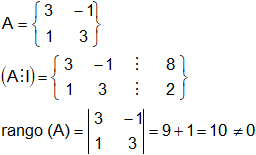
Rango (A) = 2
| rango (A ⋮ b) = | 3 | 8 | = 6 - 8 = -2 ≠ 0 |
| 1 | 2 |
Rango (A ⋮ b) = 2
Ya que rango (A) = rango (A ⋮ b) = 2 = número de incógnitas, el sistema es compatible y determinado; es decir, existe una única solución.
c)
6·x - 2·y = -10
3·x - y = -5
| A = | 6 | -2 | ||
| 3 | -1 |
| (A ⋮ b) = | 6 | -2 | ⋮ | -10 | ||
| 3 | -1 | ⋮ | -5 |
| rango (A) = | 6 | -2 | = -6 + 6 = 0 |
| 3 | -1 |
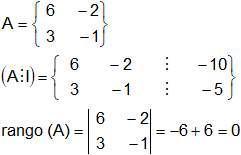
Rango (A) = 1
| rango (A ⋮ b) = | 6 | -10 | = -30 + 30 = 0 |
| 3 | -5 |
De momento, rango (A ⋮ b) = 1
| rango (A ⋮ b) = | -2 | -10 | =10 - 10 = 0 |
| -1 | -5 |
Rango (A ⋮ b) = 1
Puesto que rango (A) = rango (A ⋮ b) = 1 < número de incógnitas, el sistema es compatible e indeterminado; existen infinitas soluciones.
Autor: Jesús. España.
Editor: Ricardo Santiago Netto (Administrador de Fisicanet).