Combinaciones lineales
• Nota: En éste trabajo las letras con una raya arriba representan un vector, por ejemplo ā es el vector a.
Combinaciones lineales
Dada una familia de vectores ŭ₁, ŭ₂, ŭ₃, … y un vector cualquiera 
, se dice que es combinación lineal de la familia, si existen números reales x₁, x₂, x₃, … tales que
= x₁·ŭ₁ + x₂·ŭ₂ + x₃·ŭ₃ + …
Primera propiedad
Los vectores que son combinación lineal de un solo vector ŭ son el vector 
y todos los vectores que son paralelos a ŭ.
• Demostración:
Si es combinación lineal de ŭ, es de la forma = r·ŭ. Entonces:
a) Si r = 0, = 0·ŭ =
b) Si r ≠ 0, = r·ŭ, luego es paralelo a ŭ por tener ambos la misma dirección
Segunda propiedad
Dados dos vectores del plano ŭ₁ y ŭ₂ que tengan distinta dirección, el único vector que es combinación lineal de cada uno de ellos es el vector .
• Demostración:
Si hubiese un vector no nulo que fuese combinación lineal de cada uno de ellos, también habría de ser paralelo a cada uno de ellos, con lo que ŭ₁ y ŭ₂ han de ser paralelos entre sí, lo cual va contra la hipótesis.
Teorema.
Sean ŭ₁ y ŭ₂ dos vectores del plano con distinta dirección. Entonces cualquier vector del plano se puede poner de manera única como combinación lineal de ŭ₁ y ŭ₂
• Demostración:
- Considérese P un punto cualquiera del plano y trácense, con origen en P, representantes de los vectores ŭ₁, ŭ₂ y
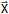
- Llamando A al extremo de 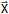, se trazan por él paralelas a los vectores ŭ₁ y ŭ₂
Prolongando las rectas que contienen a ŭ₁ y ŭ₂, se obtienen los puntos B y C.
De la figura se deduce inmediatamente que 
= 
+ 
.
Pero es paralelo a ŭ₁, por lo que se tiene que = x₁·ŭ₁, para un cierto número x₁
Análogamente = x₂·ŭ₂, para cierto escalar x₂
Por tanto = = + = x₁·ŭ₁ + x₂·ŭ₂
Falta ver la unicidad:
Si = y₁·ŭ₁ + y₂·ŭ₂, x₁·ŭ₁ + x₂·ŭ₂ = y₁·ŭ₁ + y₂·ŭ₂ ⇒ (x₁ - y₁)·ŭ₁ = (x₂ - y₂)·ŭ₂
Con lo que se tiene un vector que es combinación lineal de cada uno de ellos. Por la segunda propiedad vista anteriormente, se concluye que dicho vector ha de ser .
Así, (x₁ - y₁)·ŭ₁ = (x₂ - y₂)·ŭ₂ = . Para ello han de ser 0 los coeficientes, es decir:
| x₁ - y₁ = 0 ⇒ x₁ = y₁ x₂ - y₂ = 0 ⇒ x₂ = y₂ | Luego los números dados son únicos |
Bases coordenadas
Se llama base del plano a cualquier pareja de vectores {ŭ₁, ŭ₂} del mismo, que tengan distinta dirección.
Dados una base del plano {ŭ₁, ŭ₂} y un vector , se llama coordenadas de respecto de la base a los números reales x₁ y x₂ que verifican que = x₁·ŭ₁ + x₂·ŭ₂
Por el teorema demostrado anteriormente, las coordenadas de un vector respecto de una base existen y son únicas.
Ejercicios de aplicación
Ejemplo nº 1
Sea {ŭ₁, ŭ₂} una base del plano. Decir si las siguientes parejas de vectores son bases:
a) {2·ŭ₁ + 3·ŭ₂, 3·ŭ₁ + ŭ₂}
b) {3·ŭ₁ - 2·ŭ₂, 6·ŭ₁ - 4·ŭ₂}
Solución
Para ver si dos vectores constituyen una base hay que comprobar si tienen o no la misma dirección. Pero ya se vio que dos vectores tienen la misma dirección cuando uno de ellos es combinación lineal del otro.
a)
Hay que ver si existe un número t tal que
t·(2·ŭ₁ + 3·ŭ₂) = 3·ŭ₁ + ŭ₂
2·t·ŭ₁ + 3·t·ŭ₂ = 3·ŭ₁ + ŭ₂
Por la unicidad de las coordenadas de un vector respecto de una base se ha de verificar que:
2·t = 3 ⇒ t = 3/2
3·t = 1 ⇒ t = ⅓
Pero no hay ningún número que verifique simultáneamente ambas condiciones.
Así pues, los dos vectores tienen distinta dirección y, por tanto, constituyen una base.
b)
Se repite el proceso:
t·(3·ŭ₁ - 2·ŭ₂) = 6·ŭ₁ - 4·ŭ₂
3·t·ŭ₁ - 2·t·ŭ₂ = 6·ŭ₁ - 4·ŭ₂
Igualando coordenadas:
3·t = 6 ⇒ t = 2
-2·t = -4 ⇒ t = 2
Es un número válido para la igualdad. Los vectores dados tienen la misma dirección y, por tanto, no constituyen una base.
Ejemplo nº 2
Sea {ŭ₁, ŭ₂} una base del plano vectorial y sean x₁, x₂, y₁ e y₂ números reales.
Demostrar que el conjunto {x₁·ŭ₁ + x₂·ŭ₂, y₁·ŭ₁ + y₂·ŭ₂} es una base si x₁/y₁ ≠ x₂/y₂
Solución
Para que dos vectores ā y 
formen base, no han de ser paralelos, es decir, no ha de existir un t que verifique t ā = .
Supóngase que
t·(x₁·ŭ₁ + x₂·ŭ₂) = y₁·ŭ₁ + y₂·ŭ₂
t·x₁·ŭ₁ + t·x₂·ŭ₂ = y₁·ŭ₁ + y₂·ŭ₂
t·x₁ = y₁ ⇒ t = x₁/y₁
t·x₂ = y₂ ⇒ t = x₂/y₂
Para que los vectores no sean paralelos se ha de verificar x₁/y₁ ≠ x₂/y₂, condición impuesta.
Ejemplo nº 3
Sea {ŭ₁, ŭ₂} una base del plano. Comprobar que {2·ŭ₁ + ŭ₂, ŭ₁ - ŭ₂} es una base del plano y hallar las coordenadas del vector 5·ŭ₁ + 4·ŭ₂ respecto de dicha base.
Solución
t·(2·ŭ₁ + ŭ₂) = ŭ₁ - ŭ₂
2·t·ŭ₁ + t·ŭ₂ = ŭ₁ - ŭ₂
Igualando las coordenadas: 2·t = 1 y t = -1.
Puesto que ningún número verifica ambas condiciones, los vectores dados constituyen una base, por no ser paralelos.
Se trata ahora de calcular las coordenadas del vector 5·ŭ₁ + 4·ŭ₂ respecto de dicha base. Las coordenadas son los dos números x₁ y x₂ tales que:
5·ŭ₁ + 4·ŭ₂ = x₁·(2·ŭ₁ + ŭ₂) + x₂·(2·ŭ₁ -+ ŭ₂)
Operando en dicha igualdad:
5·ŭ₁ + 4·ŭ₂ = 2·x₁·ŭ₁ + x₁·ŭ₂ + x₂·ŭ₁ - x₂·ŭ₂ = (2·x₁ + x₂)·ŭ₁ - (x₁ - x₂)·ŭ₂
Por unicidad de las coordenadas de un vector respecto de la base {u₁, u₂}
2·x₁ + x₂ = 5 ⇒ x₂ = 5 - 2·x₁
x₁ - x₂ = 4 ⇒ x₁ = 4 + 5 - 2·x₁ ⇒ x₁ = 3
x₂ = -1
Producto escalar
Dados dos vectores no nulos del plano, se llama producto escalar al número obtenido como producto de sus módulos por el coseno del ángulo que forman:
ā· = |ā|·
·cos α
Si alguno de los dos vectores fuese el vector , su producto escalar sería igual a 0.
Propiedades del producto escalar
Primera propiedad del producto escalar
El producto escalar de dos vectores ā y es igual al producto del módulo de ā por la proyección de sobre ā (este producto será positivo si ā y la proyección de sobre él tienen el mismo signo, y negativo en caso contrario).
• Demostración:
La proyección de sobre ā es un segmento de medida x.
Por la resolución de triángulos rectángulos se sabe que cos α = x/
Sustituyendo en la definición de producto escalar:
ā· = |ā|··cos α = |ā|··(x/) = |ā|·x, que es la fórmula que se quería demostrar.
Propiedad conmutativa del producto escalar de vectores
Dados dos vectores ā y , ā· = . ā
• Demostración:
ā· = |ā|··cos α = ·|ā|·cos α = ā·
Propiedad distributiva respecto de la suma.
Dados tres vectores cualesquiera ā, y 
del plano, ā·( + ) = ā· + ā·
• Demostración:
Para demostrarlo se utiliza la primera propiedad del producto escalar.
En la figura, la proyección de sobre ā es el segmento x, la proyección de sobre ā, es el segmento y, y la proyección de + sobre ā es el segmento x + y.
Así pues:
| ā·( + ) = |ā|·(x + y) ā· = |ā|·xā· = |ā|·y | ā· + ā· = |ā|·x + |ā|·y = |ā|·(x + y) = ā·( + ) |
Propiedad de linealidad
Si se multiplica uno de los factores de un producto escalar por un número real, el producto escalar queda multiplicado por dicho número.
(x·ā). = x·(ā·)
• Demostración:
Se excluirán los casos en que alguno de los datos sea nulo. Se distinguen dos casos:
Si x > 0, |x·ā| = x·|·ā|; y x·ā tiene el mismo sentido que ā, con lo que formará con el mismo ángulo que forma con ā.
Así,
(x·ā·) = |x·ā|··cos α = x·|ā|··cos α = x·(ā·)
Si x < 0, |x·ā| = (-x)·|ā|; y por tener sentido opuesto al de ā, forma con un ángulo suplementario al que forma con ā.
Pero cos (180° - α) = -cos α, luego:
(x·ā)· = |x·ā|··cos (180° - α) = (-x)·|ā|··(-cos α) = x·|ā|··cos α = x·(ā·)
Propiedad de ortogonalidad (perpendicularidad)
Dados dos vectores no nulos ā y , si ā· = 0, entonces ā y son perpendiculares, y si ā y son perpendiculares, entonces ā· = 0
• Demostración:
a)
Como ā y son nulos, se tiene que |ā|· ≠ 0, con lo que:
ā· = 0
|ā|··cos α = 0 ⇒ cos α = 0 ⇒ α = 90°, es decir, ā ⊥
b)
Si ā y son perpendiculares, forman entre sí un ángulo de 90°, entonces
ā· = |ā|··cos 90° = |ā|··0 = 0
Positividad del producto escalar
Dado un vector cualquiera ā, ā·ā ≥ 0.
• Demostración:
Dado un vector cualquiera, se tiene que ā·ā = |ā|² (pues cos 0° = 1) y, por tanto, se tiene que ā ˆ ā ≥ 0.
El único caso en que ā ˆ ā = 0 es cuando ā =
Autor: Patricia Bati. Argentina.
Editor: Ricardo Santiago Netto (Administrador de Fisicanet).
¿Qué es el producto escalar de un número por un vector?