Derivada de una función (Segunda parte)
Cálculo de derivadas
Derivada de una función constante
Sea una función constante f(x) = C.
Su gráfica es, como se sabe, una recta paralela al eje de abscisas. Puesto que para cualquier valor de la abscisa su ordenada correspondiente es, constantemente, igual a C, si a es un punto cualquiera del campo de definición de f(x),
(a + h) - f(a) = C - C = 0, por lo que
![]()
Luego la derivada de una constante es siempre cero.
Si f(x) = C ⇒ f'(x) = 0
Derivada de la función lineal m·x + b
Sea una función lineal cualquiera f(x) = m·x + b. Para un punto cualquiera x,
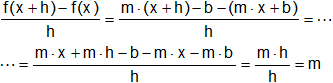
y
![]()
Lo cual significa que la derivada de una recta coincide con la pendiente de ella misma y, en consecuencia, la tangente en un punto a una recta es la propia recta.
Si f(x) = m·x + b ⇒ f'(x) = m
Derivada de una constante por una función, k·f(x)
Si k es una constante y f(x) una función, la derivada de la nueva función k·f(x) será:
| lim h ⟶ 0 | k·f(x + h) - k·f(x) | = k· | lim h ⟶ 0 | f(x + h) - f(x) | = k·f'(x) |
| h | h |
Sacando factor común k, ya que no depende de h.
Se ha demostrado que
(k·f(x))' = k·f'(x)
Así, para derivar una expresión de la forma k·f(x), basta derivar la función f(x) y multiplicar después por la constante k.
Derivada de la función xᵐ (m es un número natural)
Para calcular la derivada de la función f(x) = xᵐ, m > 0, hay que evaluar el cociente [(x + h)ᵐ - xᵐ]/h.
Desarrollando por el binomio de Newton (x + h)ᵐ,
| (x + h)ᵐ - xᵐ | = |
| h |
| = | ( | m 0 | )·xᵐ + ( | m 1 | )·xᵐ ⁻ ¹·h + ( | m 2 | )·xᵐ ⁻ ²·h² +…+ ( | m m | )·hᵐ - xᵐ | = |
| h | ||||||||||
| = | xᵐ + ( | m 1 | )·xᵐ ⁻ ¹·h +…+ ( | m m | )·hᵐ - xᵐ | = |
| h | ||||||
| = ( | m 1 | )·xᵐ ⁻ ¹ + ( | m 2 | )·xᵐ ⁻ ²·h +…+ ( | m m | )·hᵐ ⁻ ¹ |
Tomando límites cuando h ⟶ 0,
| f'(x) = | lim h ⟶ 0 | (x + h)ᵐ - xᵐ | = |
| h |
| = | lim h ⟶ 0 | [( | m 1 | )·xᵐ ⁻ ¹ + ( | m 2 | )·xᵐ ⁻ ²·h +…+ ( | m m | )·hᵐ ⁻ ¹] |
Salvo el término:
| ( | m 1 | )·xᵐ ⁻ ¹ = m·xᵐ ⁻ ¹, |
que no depende de h, el resto de los sumandos tiende a cero (su límite es cero).
Se concluye que:
Si f(x) = xᵐ ⇒ f'(x) = m·xᵐ ⁻ ¹
Ejemplo de cálculo de la derivada de la función xᵐ
Ejemplo nº 1
Calcular la derivada de f(x) = x² en el punto de abscisa - 1.
Desarrollo
Datos:
f(x) = x²
x = -1
Solución
f'(x) = 2·x² ⁻ ¹ = 2·x
f'(-1) = 2·(-1) = -2
Entonces, la pendiente de la tangente a la parábola y = x² en x = -1 es - 2.
Derivadas de las funciones trigonométricas sen x y cos x
La derivada de la función f(x) = sen x es f'(x) = cos x
La derivada de la función g(x) = cos x es g'(x) = -sen x
Las demostraciones son complejas y se pasan por alto.
Si f(x) = sen x ⇒ f'(x) = cos x
Si g(x) = cos x ⇒ g'(x) = -sen x
Derivada de la función logaritmo neperiano ln |x|
Puesto que el logaritmo está definido sólo para valores positivos y distintos de cero, es necesario considerar el logaritmo del valor absoluto de x.
Para calcular la derivada de esta función se han de considerar dos casos, x > 0 y x < 0:
a)
Si x es positivo, aun tomando h negativo, x + h es positivo si se toman valores de h suficientemente pequeños, lo cual es posible pues se va a calcular el límite cuando h tiende a cero. En estas condiciones
|x + h| = x + h y |x| = x
| ln |x + h| - ln |x| | = | ln (x + h) - ln x | = |
| h | h |
| = | 1 | ·[ln (x + h) - ln x] = | 1 | ·ln | x + h | = ln ( | x + h | )1/h |
| h | h | x | x |
Por tanto, si x > 0
| [ln (x)]' = | lim h ⟶ 0 | ln ( | x + h | )1/h = ln [ | lim h ⟶ 0 | ( | x + h | )1/h |
| x | x |
| [ln (x)]' = ln [ | lim h ⟶ 0 | (1 + | h | )1/h] |
| x |
Llamando:
h/x = n, h = n·x
| 1 | = | 1 | = | 1 | · | 1 |
| h | n·x | n | x |
Si h ⟶ 0, n ⟶ 0
| [ln (x)]' = ln [ | lim n ⟶ 0 | (1 + n)1/n | 1/x | ] = |
Recordando que:
| lim n ⟶ 0 | (1 + n)1/n = e |
[ln (x)]' = ln e1/x = (1/x)·ln e = 1/x
b)
Si x es negativo, aun tomando h positivo y suficientemente pequeño, x + h sigue siendo negativo y |x + h| = -(x + h) y |x| = -x.
(ln |x + h| - ln |x|)/h = (1/h)·{ln [-(x + h)] - ln (-x)} = (1/h)·ln [-(x + h)/(-x)] = (1/h)·ln [(x + h)/x]
Como se aprecia, se llega a la misma expresión que en el caso anterior y la demostración se continuaría de forma idéntica.
Si f(x) = ln x ⇒ f'(x) = 1/x
Derivadas de las funciones exponenciales aˣ y eˣ
Sea la función y = aˣ, siendo a una constante positiva distinta de 1. La derivada de esta función en un punto x es:
| y' = | lim h ⟶ 0 | ax + h - aˣ | = | lim h ⟶ 0 | aˣ·ah - aˣ |
| h | h |
| y' = | lim h ⟶ 0 | aˣ·(ah - 1) | = aˣ· | lim h ⟶ 0 | ah - 1 |
| h | h |
Se hace el cambio ah - 1 = t ⟶ ah = t + 1
Y se toman logaritmos neperianos:
ln ah = ln (t + 1) ⟶ h·ln a = ln (t + 1) ⟶ h = [ln (t + 1)]/ln a
Cuandoh ⟶ 0, t ⟶ a° - 1 = 0 (t ⟶ 0)
Luego:
| y' = aˣ· | lim t ⟶ 0 | t | = aˣ· | lim t ⟶ 0 | ln a |
| ln (t + 1) | (1/t)·ln (t + 1) | ||||
| ln a | |||||
| y' = aˣ·ln a | lim t ⟶ 0 | 1 |
| ln (t + 1)1/t |
Pero:
| lim t ⟶ 0 | ln (t + 1)1/t = ln | lim t ⟶ 0 | (t + 1)1/t = ln e = 1 |
y' = aˣ·ln a·(1/1) = aˣ·ln a
En particular, cuando la constante a es el número e, la derivada de la función eˣ es
(eˣ)' = eˣ·ln e = eˣ·1 = eˣ
Si f(x) = aˣ ⇒ f'(x) = aˣ·ln a
Si g(x) = eˣ ⇒ g'(x) = eˣ
Hasta el momento se saben derivar algunas funciones elementales pero no hay nada que permita encontrar las derivadas de una suma, un producto o un cociente de estas derivadas; se requiere, por consiguiente, seguir avanzando en la obtención de propiedades encaminadas a este fin.
Editor: Ricardo Santiago Netto (Administrador de Fisicanet).
¿Cuál es la derivada de una función?