• • Página de inicio
• › Análisis Matemático
• › Diferenciales
• › Teoría

Diferenciales

Teorema (Schwarz)

Sea ƒ:U ⊂ ℜ² → ℜ, U abierto, y a ∈ U. Si existen ƒ_x, ƒ_y, ƒ_xy en un entorno de a y

ƒ_xy es contínua en a, entonces existe ƒ_xy(a) y además: ƒ_yx(a) = ƒ_xy(a). Este resultado es aplicable a derivadas de orden superior.

Definición:

Decimos que una función es de clase C^m en a ∈ ℜⁿ si existen todas sus derivadas parciales hasta orden m, y además las funciones son continuas en a. Análogamente decimos que una función es de clase C^m en A ⊂ ℜⁿ si lo es en todos los puntos de A.

Definición:

Si ƒ es de clase C² en a, llamamos diferencial segunda de ƒ en a a:

Observación:

1. La diferencial segunda es una forma bilineal
2. La diferencial segunda se puede representar matricialmente:

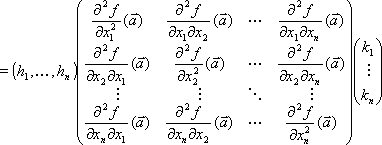
A dicha matriz se la llama Matriz hessiana o hessiano de ƒ.

Por ser ƒ de clase C², se puede aplicar Schwarz, y la matriz es simétrica.

3) Si aplicamos la diferencial segunda al mismo vector dos veces, lo que tenemos es una la forma cuadrática asociada. La podemos asimilar simbólicamente a una binomio:

En general:

Donde el exponente indica el número de veces que se ha de derivar.

Ejemplo: n = 2

Definición:

Si ƒ es de clase C^m en a, llamamos diferencial de orden m en a a:

Igualmente se puede expresar la diferencial de orden m en a como un binomio a la m.

Definición:

Sea ƒ:U ⊂ ℜⁿ → ℜ. U abierto, y ƒ de clase C^m en a. Entonces se define en polinomio de Taylor de orden m de ƒ en a como:

Y el resto de Taylor de orden m como:

ℜ_m (ƒ, a)·(x) = ƒ(x) - T_m (ƒ, a)·(x)

• ‹ Anterior
• |
• Siguiente ›

Editor: Ricardo Santiago Netto (Administrador de Fisicanet)

Ver condiciones para uso de los contenidos de fisicanet.com.ar

• 🔍
• ✉ f t