Problema nº 2-d de factorizar ecuaciones de cuarto grado, expresar en forma factorizada - TP16

Enunciado del ejercicio nº 2-d

Escribir la siguiente ecuación en la forma: aₙ·(x - xᵢ) = 0, con i = 1, 2, 3, …, n y siendo aₙ el coeficiente principal y xᵢ raíces de la ecuación.

2·x⁴ - 7·x³ + 4·x² + 7·x - 6 = 0

Desarrollo

Fórmulas:

Ecuación de Báscara o Bhaskara:

Solución

2·x⁴ - 7·x³ + 4·x² + 7·x - 6 = 0

Tenemos la ecuación planteada en forma implícita y ordenada.

Debemos buscar un binomio de primer grado para dividir la ecuación de tal forma que el resto de la división sea cero. Lo que haremos es factorizar la ecuación.

Se puede hacer un "tanteo" empleando el "teorema del resto". Descartamos "x = 0" porque a simple vista la ecuación no se anula.

Por ejemplo, el binomio "x - 1", dividimos por Ruffini:

	2	-7	4	7	-6

1		2	-5	-1	6
	2	-5	-1	6	0

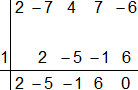
Tenemos una de las raíces:

x₁ = 1

aₙ = 2

Queda:

(x - 1)·(2·x³ - 5·x² - x + 6) = 0

Resolvemos la ecuación de tercer grado con el mismo método. Probamos con "x + 1":

2·x³ - 5·x² - x + 6

	2	-5	-1	6

-1		-2	7	-6
	2	-7	6	0

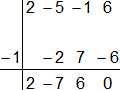
Tenemos una de las raíces:

x₂ = -1

Queda:

(x - 1)·(x + 1)·(2·x² - 7·x + 6) = 0

Luego resolvemos la ecuación de segundo grado:

2·x² - 7·x + 6 = 0

Aplicamos la ecuación de Báscara o Bhaskara, siendo:

a = 2

b = -7

c = 6

Reemplazamos y resolvemos, obtendremos dos valores:

x_3,4 =	-(-7) ± √(-7)² - 4·2·6
	2·2

x_3,4 =	7 ± √49 - 48
	4

x_3,4 =	7 ± √1
	4

x_3,4 =	7 ± 1
	4

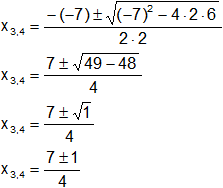
Calculamos los valores por separado según el signo del resultado de la raíz:

x₃ =	7 + 1
	4

x₃ =	8
	4

x₃ = 2

x₄ =	7 - 1
	4

x₄ =	6
	4

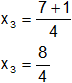
x₄ =	3
	2

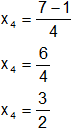
Resultado, la ecuación es:

2·(x - 1)·(x + 1)·(x - 2)·(x -	3	) = 0
	2

Resolvió: Ricardo Santiago Netto. Argentina

Ejemplo, cómo expresar ecuaciones en forma factorizada