Problema n° 3 de regresión lineal - TP04
Enunciado del ejercicio n° 3
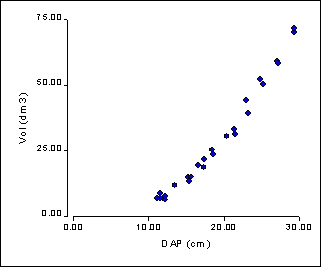
Se desea construir una tabla que permita a los productores de una localidad estimar el volumen de madera de una plantación a través de observaciones no destructivas, como contar el número de árboles y medir el diámetro del tronco. Con ese fin se estudió la relación entre el diámetro a la altura del pecho (D.A.P.) y el volumen de madera por árbol (VOL), en árboles de 14 a 16 años de edad de la especie Pinus elliotti, en la localidad de Esquina (Corrientes). Se obtuvieron las siguientes observaciones y se realizó un gráfico de dispersión.
| ARBOL | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| D.A.P. (cm) VOL (dm³) | 24,9 52,24 | 21,4 33,21 | 29,4 70,14 | 18,5 25,29 | 15,2 14,60 | 13,4 11,75 | 16,6 19,39 | 27 59,24 | 11,5 6,83 | 25,3 50,55 | 12,2 7,86 | 21,6 31,07 | 23,2 39,31 | 15,4 13,24 |
| ARBOL | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| D.A.P. (cm) VOL (dm³) | 27,2 58,30 | 17,3 18,67 | 11,1 7,11 | 29,4 71,56 | 18,6 23,70 | 20,4 30,35 | 23 43,95 | 11,5 8,69 | 15,7 15,09 | 17,4 21,55 | 12,2 6,33 |
El análisis de regresión produjo los siguientes resultados:
| R² = 0,9676 | Coeficientes | Error standard | t Student | Probabilidad |
|---|---|---|---|---|
| Intercepción | -37,044 | 2,6535 | -13,9602 | 1,0204·10-12 |
| Pendiente | 3,4754 | 0,1326 | 26,2090 | 1,24153·10-18 |
Estadísticas de la regresión
| Coeficiente de correlación múltiple Coeficiente de determinación R² R² ajustado Error típico Observaciones | 0,983667767 0,967602277 0,96619368 3,792909771 25 |
Análisis de varianza
| Grados de libertad | Suma de cuadrados | Promedio de los cuadrados | F | Valor crítico de F | |
| Regresión | 1 | 9882,2366 | 9882,2366 | 686,926427 | 1,2412·10-18 |
| Residuos | 23 | 330,8817841 | 14,3861645 | ||
| Total | 24 | 10.213,11838 |
| Coeficientes | Error típico | Estadístico t | Probabilidad | Inferior 95 % | Superior 95,0 % | |
| Intercepción | -37,04788413 | 2,653676876 | -13,9609628 | 1,0192·10-12 | -42,5374255 | -31,5583427 |
| D.A.P. (cm) (x) | 3,47563017 | 0,132610663 | 26,2092813 | 1,2412·10-18 | 3,20130449 | 3,74995585 |
Análisis de los residuales
| Observación | Pronóstico VOL (dm³) (y) | Residuos |
| 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 | 49,49530709 37,3306015 65,13564285 27,25127401 15,78169445 9,525560141 20,64757668 56,79413045 2,921862819 50,88555916 5,354803937 38,02572753 43,5867358 16,47682048 57,48925648 23,0805178 1,531610751 65,13564285 27,59883702 33,85497133 42,89160977 2,921862819 17,51950953 23,42808082 5,354803937 | 2,74469291 -4,120601497 5,004357147 -1,961274005 -1,181694446 2,224439859 -1,257576683 2,445869554 3,908137181 -0,335559158 2,505196063 -6,955727531 -4,276735802 -3,23682048 0,81074352 -4,410517802 5,578389249 6,424357147 -3,898837022 -3,504971327 1,058390232 5,768137181 -2,429509531 -1,878080819 0,975196063 |
Presente el modelo de regresión lineal estimado para predecir el volumen por árbol en función del diámetro del tronco. Identifique los estimadores de los parámetros y las variables explicativa y de respuesta.
Yi = β0 + β1·Xi + εi
Con Yi = volumen del arbol (variable respuesta)
Xi = diámetro del tronco (variable explicativa)
b0 = estimador de ordenada al origen = -37,044
b1 = estimador de pendiente = 3,4754
Proponga hipótesis de interés para poner a prueba y comente los resultados.
H0: β1 = 0; H1: β1 ≠ 0.
Dado que el valor p = 1,2412·10-18 la pendiente es significativa.
¿Qué interpretación biológica puede darse a una pendiente significativa de 3,475 en este contexto?
Que ante un aumento de 1 cm en el diámetro del árbol, se obtendrá un aumento de 3,475 dm³ en el volumen del árbol.
¿Qué indica un coeficiente de determinación (R²) igual a 0,9676?
Que el 96,76 % de las variaciones en el volumen están explicadas por las variaciones en el diámetro del árbol.
Calcule el valor estimado y el residual de la observación correspondiente al árbol 16.
Y(16) esperado = -37,044 + 3,4754·17,3 = 23,08042
Y(16) observado = 18,67
e(16) = 18,67 - 23,08042 = -4,41042
¿Se puede afirmar, con una probabilidad de error del 5 %, que el volumen de madera aumenta significativamente cuando el D.A.P. aumenta?
H0: β1 = 0 vs. H1: β1 ≠ 0.
Si H0 es cierta, entonces se estima que no existe asociación alguna entre X e Y.
tc = (b1 - β1)/s(b1) = (3,4754 - 0)/0,1326 = 26,20
Tiene distribución tn - 2 para el modelo que estamos utilizando, luego t tabla = tn - 2; α/2 = t23; 0,025 = 2,068654794
Como t calculado > t tabla rechazo Ho entonces hay regresión.
Calcule un IC90 para la pendiente del modelo.
P{b1 - t(α/2; n - 2)·s(b1) ≤ β1 ≤ b1 + t(α/2; n - 2)·s(b1)} = 1 - α
Con b = 3,4754
S(b1) = 0,1326
tαn - 2; α/2 = t23; 0,025 = 1,713870006
| 3,24835273 | 3,70290761 |
Autor: Olga Susana Filippini. Argentina.
Editor: Ricardo Santiago Netto (Administrador de Fisicanet)
- ‹ Anterior |
- Regresar a la guía TP04
- | Siguiente ›
Ejemplo, cómo analizar la regresión lineal, el gráfico de dispersión y cómo calcular la varianza