Problema nº 14 de estadística descriptiva ocurrencia de un suceso - TP07
Enunciado del ejercicio nº 14
Se conoce que la variable frecuencia relativa de abonados en un instante dado en la cola de espera de un servicio en una empresa sigue una distribución cuya función de densidad es f(t) = t² - 2·t + (5/3).
a) Graficar f(t) y verificar que f(t) es una función de densidad.
b) Calcular la media y la variancia de t.
c) Calcular la probabilidad de que en un instante dado haya en la cola de espera al menos un 30 % de abonados.
Solución
a)
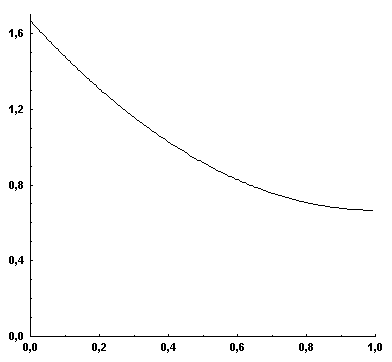
Gráfico de frecuencia relativa
f(t) ≥ 0 en [0;1] y
| ∫ | 1 | f(t)·dt = ∫ | 1 | (t² - 2·t + 5/3)·dt = |
| 0 | 0 |
| = [⅓·t³ - 2·½·t² + (5/3)·t] | 1 | = |
| 0 |
= ⅓ - 1 + (5/3) = 1
b)
| μ = ∫ | 1 | t·f(t)·dt = ∫ | 1 | [t³ - 2·t² + (5/3)·t]·dt |
| 0 | 0 |
| μ = [¼·t⁴ - 2·⅓·t³ + (5/3)·½·t²] | 1 |
| 0 |
μ = ¼ - ⅔ + ⅚
μ = 5/12
μ = 0,417
| σ² = ∫ | 1 | t²·f(t)·dt - μ² |
| 0 |
| σ² = ∫ | 1 | [t⁴ - 2·t³ + (5/3)·t²]·dt - μ² |
| 0 |
| σ² = [⅕·t⁵ - 2·¼·t⁴ + (5/3)·⅓·t³] | 1 | - (5/12)² |
| 0 |
σ² = 23/90 - 25/144
σ² = 0,0819
c)
| F(t) = ∫ | t | f(x)·dx = ∫ | t | (x² - 2·x + 5/3)·dx |
| 1 | 1 |
| F(t) = [⅓·x³ - 2·½·x² + (5/3)·x] | t |
| 1 |
F(t) = ⅓·t³ - t² + (5/3)·t
Luego F(0,30) = 0,419 y
P(X > 0,30) = 1 - 0,419 = 0,581
P(X > 0,30) = 0,581
Autor: Olga Susana Filippini. Argentina.
Editor: Ricardo Santiago Netto (Administrador de Fisicanet).
- ‹ Anterior |
- Regresar a la guía TP07
- | Siguiente ›
Ejemplo, cómo calcular la probabilidad de que ocurra un suceso