Función exponencial

Tradicionalmente, el estudio de los logaritmos ha ido inevitablemente acompañado de las tablas logarítmicas y del estudio de conceptos tales como el de mantisa, característica, cologaritmo …

Hoy en día esto ya no es necesario. Con la creciente utilización de las calculadoras en todos los niveles, el cálculo logarítmico se ha simplificado enormemente.

Por tanto, en este tema se prescindirá del manejo de las tablas y de su explicación.

La invención de los logaritmos (palabra de origen griego: logos (logos) = tratado, arithmos (αriqmos) = números), se debe al matemático escocés John Napier, barón de Merchiston (1.550 - 1.617), quien se interesó fundamentalmente por el cálculo numérico y la trigonometría. En 1.614, y tras veinte años de trabajo, publicó su obra Logarithmorum canonis descriptio, donde explica cómo se utilizan los logaritmos, pero no relata el proceso que le llevó a ellos.

Un año después, en 1.615, el matemático inglés Henry Briggs (1.561 - 1.631), visitó a John Napier o Neper y le sugirió utilizar como base de los logaritmos el número 10. A Napier le agradó la idea y se comprometieron a elaborar las tablas de los logaritmos decimales. Napier muere al cabo de dos años escasos y se queda Briggs con la tarea.

En 1.618, Briggs publicó Logarithmorum Chiliaes prima, primer tratado sobre los logaritmos vulgares o de Briggs, cuya base es el número 10. Briggs hizo el cálculo de las tablas de logaritmos de 1 a 20.000 y de 90.000 a 100.000.

En 1.620, el hijo de Napier publicó la obra de su padre Mirifici logarithmorum canonis constructio («Descripción de la maravillosa regla de los logaritmos») donde ya se explica el proceso seguido por Napier, mediante la comparación de progresiones y la utilización de unas varillas cifradas, llamadas varillas o regletas de Napier, para llegar a sus resultados sobre los logaritmos.

Las tablas de los logaritmos decimales de Briggs fueron completadas de 1 a 100.000 en 1.628 por el matemático Vlacq.

Estos resultados fueron muy bien acogidos por el mundo científico del momento, que no dudó en utilizarlos para la resolución de cálculos numéricos.

Función exponencial

Se llama función exponencial de base a, siendo a un número real positivo y distinto de 1, a la función:

f:ℜ ⟶ ℜ

x ⟶ f(x) = aˣ

Esta función se escribe también como f(x) = expₐ x y se lee «exponencial en base a de x».

Antes de dar un ejemplo de función exponencial, conviene recordar algunas propiedades de las potencias:

1) a° = 1

2) a⁻ⁿ = 1/aⁿ

3) a^m/n =

4) a⁻m/n =	1	=	1
	am/n

Ejemplos de funciones exponenciales

Ejemplo nº 1

La función y = 2ˣ es una función exponencial de base 2. Algunos de los valores que toma esta función, f:ℜ ⟶ ℜ

f(-3) = 2⁻³ = ½³ = ⅛

f(-½) = 2⁻^½ = ½^½ = 1/√2

f(1) = 2¹ = 2

f(3/2) = 2^3/2 = √2³ = √8

Ejemplo nº 2

La función y = ½ˣ es una función exponencial de base ½.

Alguno de los valores que toma esta función, f:ℜ ⟶ ℜ, son:

f(-4) = 2⁻⁴ = ½⁴ = 1/16

f(0) = ½° = 1

f(2) = ½² = ¼

Propiedades de la función exponencial y = aˣ

1) Para x = 0, la función toma el valor 1: f(0) = a° = 1

2) Para x = 1, la función toma el valor a: f(1) = a¹ = a

3) La función es positiva para cualquier valor de x: f(x) > 0.
Esto es debido a que la base de la potencia, a, es positiva, y cualquier potencia de base positiva da como resultado un número positivo.

4) Si la base de la potencia es mayor que 1, a > 1, la función es creciente.

5) Si la base de la potencia es menor que 1, a < 1, la función es decreciente.

Representación gráfica de la función exponencial

Observando las propiedades antes descritas para una función exponencial, se han de distinguir dos casos para hacer la representación de una función y = aˣ:

a)

a > 1

En este caso, para x = 0, y = a° = 1

Para x = 1, y = a¹ = a

Para cualquier x, la función es creciente y siempre positiva.

Como caso particular se representa la función y = 2ˣ

b)

a < 1

Para x = 0, y = a° = 1

Para x = 1, y = a¹ = a

Para cualquier x la función es decreciente y siempre positiva.

Como caso particular se representa la función y = ½ˣ

Ecuaciones y sistemas de ecuaciones exponenciales

Las ecuaciones en las que la incógnita aparece como exponente son ecuaciones exponenciales.

No hay ninguna fórmula general que indique cómo resolver cualquier ecuación exponencial. Sólo la práctica ayuda a decidir, en cada caso, qué camino tomar.

Para resolver estas ecuaciones hay que tener presente algunos resultados y propiedades:

1) aˣ = aʸ ⇔ x = y

Conviene, por tanto, siempre que sea posible, expresar los dos miembros de la ecuación como potencias de la misma base.

2) aˣ·aʸ = aˣ ⁺ ʸ

3) aˣ/aʸ = aˣ ⁻ ʸ

4) (aˣ)ʸ = aˣ˙ʸ

El uso de los logaritmos, como se verá más adelante, facilita en muchas ocasiones la resolución de estas ecuaciones.

Ejemplo de resolución de ecuaciones exponenciales

Ejemplo nº 1

Resolver 2^{1 - x²} = ⅛

Solución

Expresando ⅛ como potencia de 2: 2^{1 - x²} = ½³

2^{1 - x²} = 2⁻³ ⇒ 1 - x² = -3

Basta ahora con resolver esta ecuación de segundo grado.

1 - x² = -3 ⟶ x² = 4 ⟶ x = ± 2

Ejemplo nº 5

Resolver 4ˣ ⁺ ¹ + 2ˣ ⁺ ³ = 320

Solución

En algunas ecuaciones es necesario hacer un cambio de variable para su resolución.

Teniendo en cuenta las propiedades de las potencias, la ecuación puede escribirse:

4·4ˣ + 2³·2ˣ = 320 ⟶ 4·4ˣ + 8·2ˣ = 320

Expresando 4ˣ como potencia de dos,

4·2²˙ˣ + 8·2ˣ = 320

Se hace el cambio de variable 2ˣ = y, (por tanto 2²˙ˣ = y²) y se obtiene:

4·y² + 8·y = 320

Basta ahora con resolver esta ecuación:

y² + 2·y - 80 = 0

Siendo:

a = 1

b = 2

c = -80

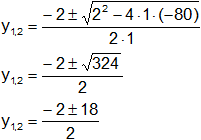
y₁ = -10

y₂ = 8

Se deshace ahora el cambio y = 2ˣ

y₁ = -10 = 2ˣ. No es posible encontrar un "x" que verifique esta condición (2ˣ es siempre positivo)

y₂ = 8 = 2ˣ ⟶ x = 3

La solución es, por tanto, x = 3

Ejemplo nº 3

Resolver 5ˣ + 5ˣ ⁺ ² + 5ˣ ⁺ ⁴ = 651

Solución

Aplicando las propiedades de las potencias, la ecuación se puede escribir como

5ˣ + 5²·5ˣ + 5⁴·5ˣ = 651

Sacando factor común 5ˣ:

5ˣ·(1 + 5² + 5⁴) = 651

5ˣ·651 = 651 ⟶ 5ˣ = 1 ⟶ x = 0

Algunas ecuaciones exponenciales requieren, para su resolución, el empleo de logaritmos y por ello se tratarán junto con las ecuaciones logarítmicas.

Ejemplo de resolución de sistemas de ecuaciones exponenciales

Ejemplo nº 1

Resolver el sistema:

2ˣ - 4²˙ʸ = 0
x - y = 15

Solución

Se despeja "x" en la segunda ecuación:

x = 15 + y

Se sustituye este valor de x en la primera ecuación:

2¹⁵ ⁺ ʸ - 4²˙ʸ = 0 (pero 4 = 2²)

2¹⁵ ⁺ ʸ - (2²)²˙ʸ = 0

2¹⁵ ⁺ ʸ - 2⁴˙ʸ = 0 ⇒ 2¹⁵ ⁺ ʸ = 2⁴˙ʸ ⇒ 15 + y = 4·y ⇒ 3 y = 15 ⇒ y = 5

Se sustituye el valor de y = 5 en x = 15 + y:

x = 15 + 5 = 20

Por tanto, y = 5; x = 20

Ejemplo nº 2

Resolver el sistema:

2^{2·x + 5·y} = 2
2⁻ˣ ⁺ ʸ = 8

Solución

Se ponen todos los factores como potencia de base 2:

2^{2·x + 5·y} = 2¹ ⇒ 2·x + 5·y = 1

2⁻ˣ ⁺ ʸ = 2³ ⇒ -x + y = 3

Resolviendo este sistema de ecuaciones por cualquier método resulta,

x = -2; y = 1

Ejemplo nº 3

Resolver el sistema:

2ˣ + 2ʸ = 24
2ˣ·2ʸ = 128

Solución

Para obtener los valores de "x" e "y" hay que deshacer el cambio:

a = 8 ⇒ 2ˣ = 8 ⇒ 2ˣ = 2³ ⇒ x = 3

b = 16 ⇒ 2ʸ = 16 ⇒ 2ʸ = 2⁴ ⇒ y = 4

Logaritmos

Dado un número real a positivo, no nulo y distinto de 1, (a > 0; a ≠ 0; a ≠ 1), y un número N positivo y no nulo (N > 0; N ≠ 0), se llama logaritmo en base a de N al exponente x al que hay que elevar dicha base para obtener el número.

Para indicar que x es el logaritmo en base a de N se escribe:

logₐ N = x

Se lee «logaritmo en base a de N es igual a x».

Por lo tanto, logₐ N = x (notación logarítmica) equivale a decir que aˣ = N (notación exponencial).

Consecuencias de la definición de logaritmo

1) El logaritmo de 1, en cualquier base, es 0: logₐ 1 = 0, ya que a° = 1

2) El logaritmo de un número igual a la base es 1: logₐ a = 1, ya que a¹ = a

3) El logaritmo de una potencia cuya base es igual a la base del logaritmo es igual al exponente de la potencia: logₐ aᵐ = m, ya que aᵐ = aᵐ

4) No existe el logaritmo en cualquier base de un número negativo o cero.

5) El logaritmo de un número N mayor que cero y menor que 1, estrictamente, 0 < N < 1, es negativo si la base a del logaritmo es a > 1.
Así, por ejemplo, log₃ ⅑ = -2, ya que 3⁻² = ⅑

6) El logaritmo de un número N mayor que cero y menor que 1, estrictamente, 0 < N < 1, es positivo si la base a del logaritmo es a < 1.
Por ejemplo, log_⅓ ⅑ = 2, ya que ⅓² = ⅑

7) El logaritmo de un número N > 1 es positivo si la base es a > 1.
Así, log₃ 9 = 2; ya que 3² = 9

8) El logaritmo de un número N > 1 es negativo si la base es a < 1.
Así, log_⅕ 25 = -2, ya que (⅕)⁻² = 25

Propiedades de los logaritmos

1. Logaritmo de un producto

El logaritmo de un producto de dos números es igual a la suma de los logaritmos de cada uno de ellos.

logₐ(X·Y) = logₐ X + logₐ Y

• Demostración:

Sea logₐ X = x; esto significa que aˣ = X.

Sea logₐ Y = y; esto significa que aʸ = Y.

logₐ(X·Y) = logₐ (aˣ·aʸ) = logₐ aˣ ⁺ ʸ = x + y = logₐ X + logₐ Y

Este resultado se puede generalizar para más de dos factores.

Si X₁, X₂, X₃, …, Xₙ son n números reales, positivos y no nulos,

logₐ(X₁·X₂ … Xₙ) = logₐ X₁ + logₐ X₂ + … + logₐ Xₙ

2. Logaritmo de un cociente

El logaritmo de un cociente de dos números es igual al logaritmo del numerador menos el logaritmo del denominador.

logₐ X/Y = logₐ X - logₐ Y

• Demostración:

Sea logₐ X = x; esto significa que aˣ = X

Sea logₐ Y = y; esto significa que aʸ = Y

logₐ (X/Y) = logₐ (aˣ/aʸ) = logₐ (aˣ ⁻ ʸ) = x - y = logₐ X - logₐ Y

3. Logaritmo de una potencia

El logaritmo de una potencia es igual al exponente multiplicado por el logaritmo de la base de la potencia.

logₐ Xⁿ = n·logₐ X

• Demostración:

Sea logₐ X = x; esto significa que aˣ = X.

logₐ Xⁿ = logₐ (aˣ)ⁿ = logₐ aⁿ˙ˣ = n·x = n·logₐ X

4. Logaritmo de una raíz

El logaritmo de una raíz es igual al logaritmo del radicando dividido entre el índice de la raíz.

logₐ =	1	·logₐ X
	n

• Demostración:

Este es un caso particular del apartado anterior, logaritmo de una potencia.

logₐ = logₐ X1/n =	1	·logₐ X
	n

Obsérvese que las propiedades anteriores se refieren al logaritmo de un producto, un cociente, una potencia y una raíz, pero nada se ha dicho sobre el logaritmo de una suma o una resta. El logaritmo de una suma o de una resta no admite desarrollo.

Editor: Ricardo Santiago Netto (Administrador de Fisicanet).

• ‹ Anterior
• |
• Siguiente ›