Función logarítmica (primera parte)
Ejemplos de cálculo de logaritmos
Ejemplo nº 1
Sabiendo que log₁₀ 2 = 0,301030 y log₁₀ 3 = 0,477121, calcular log₁₀ 6, log₁₀ 8, log₁₀ 3/2, ![]()
Solución
Para obtener los logaritmos pedidos a partir del logaritmo de 2 y de 3, hay que expresar los números 6; 8; 3/2 y 3,6 en función de 2 y 3.
log₁₀ 6 = log₁₀ (2·3)
log₁₀ 6 = log₁₀ 2 + log₁₀ 3
log₁₀ 6 = 0,301030 + 0,477121
log₁₀ 6 = 0,778151
log₁₀ 8 = log₁₀ 2³
log₁₀ 8 = 3·log₁₀ 2
log₁₀ 8 = 3·0,301030
log₁₀ 8 = 0,903090
log₁₀ 3/2 = log₁₀ 3 - log₁₀ 2
log₁₀ 3/2 = 0,477121 - 0,301030
log₁₀ 3/2 = 0,146091

Ejemplo nº 2
Calcular log₂ 64, log½ 4, log₇ ⅐
Solución
log₂ 64 = log₂ 2⁶ = 6·log₂ 2 = 6·1 = 6
log½ 4 = log½ ½⁻² = -2
log₇ ⅐ = log₇ 1 - log₇ 7 = 0 - 1 = -1
Ejemplo nº 3
Desarrollar el logaritmo de la expresión:
![]()
Solución
El desarrollo del logaritmo es independiente de la base que se tome, por lo tanto, se prescindirá de ella.
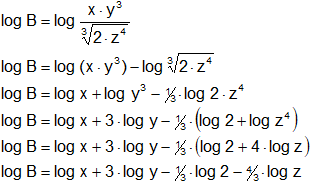
Ejemplo nº 4
Desarrollar el logaritmo de la expresión:
![]()
Solución
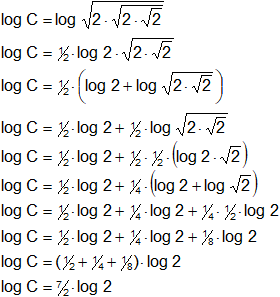
Ejemplo nº 5
Obtener la expresión de E a partir del desarrollo de su logaritmo:
log E = 3·log x + 2·log y - ½·log z
Solución
En este caso se trata de hacer el proceso inverso que en los casos anteriores.
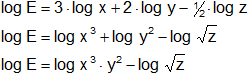
Por lo tanto, sí:
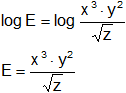
Ejemplo nº 6
Calcular x para que cada una de las siguientes expresiones sea cierta:
logₓ 8 = ½; logₓ ⅑ = -2; log₂₇ x = ⅓; log₁₀ 0,01 = x; log½ x = -1
Solución
logₓ 8 = ½ ⇒ x½ = 8 ⇒ ![]() ⇒ x = 8² ⇒ x = 64
⇒ x = 8² ⇒ x = 64
logₓ ⅑ = -2 ⇒ x⁻² = ⅑ ⇒ 1/x² = ⅑ ⇒ x² = 9 ⇒ x = 3
log₂₇ x = ⅓ ⇒ 27⅓ = x ⇒ ![]() ⇒ x = 3
⇒ x = 3
log₁₀ 0,01 = x ⇒ 10ˣ = 0,01 ⇒ 10ˣ = 1/100 ⇒ 10ˣ = ⅒² = 10⁻² ⇒ x = -2
log½ x = -1 ⇒ ½⁻¹ = x ⇒ x = 2
Logaritmos decimales y logaritmos naturales
De todas las posibles bases que pueden tomarse para los logaritmos, las más usuales son la base 10 y la base e.
Los logaritmos que tienen base 10 se llaman logaritmos decimales, logaritmos vulgares o logaritmos de Briggs, y para representarlos se escribe sencillamente log sin necesidad de especificar la base:
log₁₀ X = log X
Las tablas que tradicionalmente se han usado para calcular logaritmos, son tablas de logaritmos decimales.
Se escriben a continuación algunos ejemplos de logaritmos decimales:
log 1 = 0; puesto que 10° = 1 ⟶ log 10.000 = 4; puesto que 10⁴ = 10.000.
log 10 = 1; puesto que 10¹ = 10 ⟶ log 0,1 = -1; puesto que 10⁻¹ = 0,1.
Los logaritmos que tienen base e se llaman logaritmos neperianos o naturales. Para representarlos se escribe ln o bien L:
logₑ X = ln X = LX
Algunos ejemplos de logaritmos neperianos son:
ln 1 = 0; puesto que e° = 1
ln e² = 2; puesto que e² = e²
ln e⁻¹ = -1; puesto que e⁻¹ = e⁻¹
El número e tiene gran importancia en Matemática. No es racional (no es cociente de dos números enteros) y es el límite de la sucesión
![]() , es decir:
, es decir:
![]()
Su valor, con seis cifras decimales, es:
e = 2,718281…
Cambio de base
Para un mismo número X existen infinitos logaritmos, dependiendo de la base que se tome.
Por ejemplo, el logaritmo de 8 es 1, -1, 3, -3, 0,903090, 2,079441 … según que la base considerada sea 8, ⅛, 2, ½, 10, e …
Es posible pasar del logaritmo de un número en una base "a" determinada al logaritmo de ese mismo número en otra base "b", sin más que aplicar la siguiente fórmula:
logb x = logₐ x/logₐ b
• Demostración:
Sea:
Tomando logaritmos en base a en la igualdad anterior, se tiene:
logₐ aA = logₐ bB ⇒ A·logₐ a = B·logₐ b
Despejando B, y teniendo en cuenta que logₐ a = 1, se tiene:
B = A/logₐ b
Es decir,
logb x = logₐ x/logₐ b
Ejemplos de cambios de base de logaritmos
Ejemplo nº 1
Sabiendo que log₂ 8 = 3, calcular log₁₆ 8
Solución
Aplicando la fórmula, log₁₆ 8 = log₂ 8/log₂ 16 = ¾ = 0,75
Ejemplo nº 2
Sabiendo que log₃ 27 = 3, calcular log₉ 27
Solución
log₉ 27 = log₃ 27/log₃ 9 = 3/2 = 1,5
Ejemplo nº 3
Sabiendo que log 2 = 0,301030 y log 7 = 0,845098, calcular log₇ 2.
Solución
log₇ 2 = log 2/log 7 = 0,301030/0,845098 = 0,356207
Relación entre logaritmos decimales y neperianos
Conocido el logaritmo decimal de un número, la fórmula que permite obtener su logaritmo neperiano es:
ln X = log X/log e, donde log e = 0,434294
Conocido el logaritmo neperiano de un número, la fórmula que permite obtener su logaritmo decimal es:
ln X = ln X/ln 10, donde ln 10 = 2,302585
Relación entre los logaritmos en base a y en base 1/a
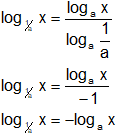
log1/a X = -logₐ X
Relación entre logₐ b y logb a
logb a = logₐ a/logₐ b = 1/logₐ b
Los logaritmos logₐ b y logb a son inversos.
Ejemplos de cambio de base de logaritmos inversos
Ejemplo nº 1
Dado el log 25 = 1,397940, calcular ln 25.
Solución
ln 25 = log 25/log e = 1,397940/0,434294 = 3,218879
Ejemplo nº 2
Dado el ln 17 = 2,833213, calcular log 17.
Solución
log 17 = ln 17/ln 10 = 2,833213/2,302585 = 1,230448
Ejemplo nº 3
Calcular log⅙ 216, sabiendo que log₆ 216 = 3.
Solución
log⅙ 216 = -log₆ 216 = -3
Ejemplo nº 4
Calcular log₃ 10, sabiendo que log 3 = 0,477121.
Solución
log₃ 10 = 1/log 3 = 1/0,477121 = 2,095904
Ejemplo nº 5
Calcular log₅ e, sabiendo que ln 5 = 1,609437.
Solución
log₅ e = 1/ln 5 = 1/1,609437 = 0,621335
Editor: Ricardo Santiago Netto (Administrador de Fisicanet).