Problema nº 2 de funciones lineales, resolver y graficar sistemas de ecuaciones lineales - TP01

Enunciado del ejercicio nº 2

Hallar las ecuaciones implícita y explícita de las siguientes rectas y graficar:

a) Pasa por el punto P(2; 2) y es paralela a la recta de ecuación 3·x - 2·y + 1 = 0.

b) Pasa por el punto P(-1; 3) y es perpendicular a la recta de ecuación -3·x/2 + 5·y/6 - 8 = 2.

c) r₁ pasa por el punto Q₁(2; 3) y r₂ pasa por el punto Q₂(-2; -3), sabiendo que son perpendiculares.

Desarrollo

Datos:

P(2; 2)

3·x - 2·y + 1 = 0

Solución

Expresamos la segunda recta en forma explícita:

3·x - 2·y + 1 = 0

3·x + 1 = 2·y

2·y = 3·x + 1

y = (3·x + 1)/2

y = 3·x/2 + ½

La pendiente de la segunda recta es:

m₂ = 3/2

La ordenada al origen es:

b₂ = ½

Si la recta buscada es paralela a la segunda recta, entonces:

m₁ = m₂

Ahora utilizamos la fórmula para generar la ecuación de una recta con la pendiente y un punto:

y - y₁ = m₁·(x - x₁)

Reemplazando:

y - 2 = (3/2)·(x - 2)

y - 2 = (3/2)·x - (3/2)·2

y - 2 = 3·x/2 - 3

y = 3·x/2 - 3 + 2

Resultado, la ecuación explícita es:

y = 3·x/2 - 1

m₁ = 3/2

b₁ = -1

Resultado, la ecuación implícita es:

y - 3·x/2 + 1 = 0

La gráfica es:

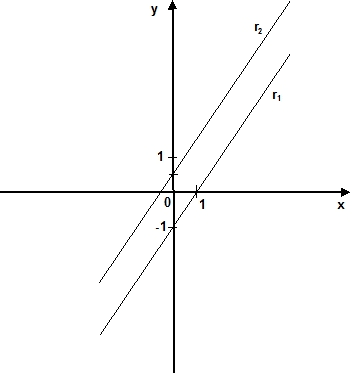
Gráfica de rectas paralelas

Desarrollo

Datos:

P(-1; 3)

-3·x/2 + 5·y/6 - 8 = 2

Solución

Expresamos la segunda recta en forma explícita:

-3·x/2 + 5·y/6 = 8 + 2

5·y/6 = 3·x/2 + 10

y = 6·(3·x/2 + 10)/5

y = (18·x/2 + 60)/5

y = (9·x + 60)/5

y = 9·x/5 + 60/5

y = 9·x/5 + 12

La pendiente de la segunda recta es:

m₂ = 9/5

La ordenada al origen es:

b₂ = 12

Si la recta buscada es perpendicular a la segunda recta, entonces:

m₁ ⊥ m₂ ⇒ m₁ = -1/m₂

Entonces:

m₁ = -1/(9/5) = -5/9

Ahora utilizamos la fórmula para generar la ecuación de una recta con la pendiente y un punto:

y - y₁ = m₁·(x - x₁)

Reemplazando:

y - 3 = (-5/9)·(x - (-1))

y - 3 = (-5/9)·(x + 1)

y - 3 = -5·x/9 - 5/9

y = -5·x/9 - 5/9 + 3

y = -5·x/9 + (- 5 + 3·9)/9

y = -5·x/9 + (- 5 + 27)/9

Resultado, la ecuación explícita es:

y = -5·x/9 + 22/9

m₁ = -5/9

b₁ = 22/9

Resultado, la ecuación implícita es:

y + 5·x/9 - 22/9 = 0

La gráfica es:

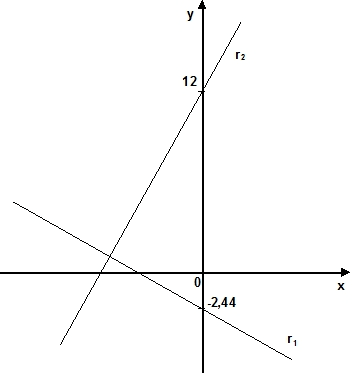
Gráfica de rectas perpendiculares

Desarrollo

Datos:

Q₁(2; 3)

Q₂(-2; -3)

r₁ ⊥ r₂

Solución

Dado que las rectas son perpendiculares, sus pendientes son:

m₁ = -1/m₂

r₁: y - y₁ = m₁·(x - x₁)

r₂: y - y₂ = m₂·(x - x₂) ⇒ y - y₂ = (-1/m₁)·(x - x₂)

r₁: y - 3 = m₁·(x - 2)

r₂: y - (-3) = (-1/m₁)·[x - (-2)] ⇒ y + 3 = (-1/m₁)·(x + 2)

Despejamos la pendiente m₁ de la ecuación r₁:

r₁: y - 3 = m₁·(x - 2)

m₁ = (y - 3)/(x - 2) (1)

Y la reemplazamos en la ecuación de r₂:

y + 3 = {-1/[(y - 3)/(x - 2)]}·(x + 2)

Luego resolvemos algebraicamente:

y + 3 = [-(x - 2)/(y - 3)]·(x + 2)

(y + 3)·(y - 3) = -(x - 2)·(x + 2) (2)

y² - 3² = -(x² - 2²)

y² - 9 = -(x² - 4)

y² - 9 = -x² + 4

y² + x² = 4 + 9

y² + x² = 13

Todos los puntos que satisfagan ésta ecuación corresponden a rectas perpendiculares que pasan por los puntos citados. Observando la ecuación (2) obtenemos los puntos que cumplen con la ecuación.

Para y = 3, tenemos:

(3)² + x² = 13

9 + x² = 13

x² = 13 - 9

x² = 4

x₁ = 2

x₂ = -2

Formamos los puntos:

Q₁(2; 3) se descarta, está dado en el enunciado.

P₁(-2; 3)

Para y = -3, tenemos:

(-3)² + x² = 13

9 + x² = 13

x² = 13 - 9

x² = 4

x₁ = 2

x₂ = -2

Formamos los puntos:

Q₂(-2; -3) se descarta, está dado en el enunciado.

P₂(2; -3)

P₁ y P₂ son puntos de intersección de distintos pares de rectas perpendiculares, con cualquiera de ellos y los datos del enunciado podemos formar un par de rectas perpendiculares que pasen por los puntos Q₁ y Q₂

Tomemos P₂ y reemplacemos en la ecuación de la pendiente (2):

m₁ = (y - 3)/(x - 2)

m₁ = (-3 - 3)/(2 - 2)

m₁ = -6/0 ⟶ ∞

¡Solución indeterminada! Correcto una pendiente es paralela al eje Y.

Usemos P₁ y reemplacemos en la ecuación (2):

m₁ = (y - 3)/(x - 2)

m₁ = (3 - 3)/(-2 - 2)

m₁ = -0/4 ⟶ 0

Pendiente paralela el eje X, cumple con la condición de perpendicularidad.

Las ecuaciones de las rectas serán:

r₁: y - 3 = m₁·(x - 2)

r₁: y - 3 = 0·(x - 2)

Resultado, la ecuación implícita es:

r₁: y - 3 = 0

Resultado, la ecuación explícita es:

r₁: y = 3 (paralela el eje X)

r₂: y + 3 = (-1/m₁)·(x + 2)

r₂: (y + 3)·(-m₁) = x + 2

r₂: (y + 3)·0 = x + 2

Resultado, la ecuación implícita es:

r₂: 0 = x + 2

Resultado, la ecuación explícita es:

r₂: x = -2 (paralela el eje Y)

• Los invito a probar con la pendiente inversa (m₂).

La gráfica es:

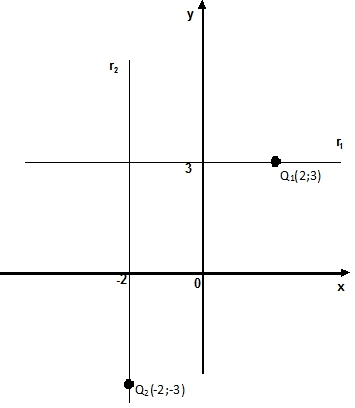
Gráfica de rectas perpendiculares

Resolvió: Ricardo Santiago Netto. Argentina

Ejemplo, cómo resolver y graficar sistemas de ecuaciones lineales