Problema nº 1-c de funciones lineales, hallar y graficar rectas - TP01

Enunciado del ejercicio nº 1-c

Hallar la ecuación general de la recta que en el plano XY satisface las siguientes condiciones, graficar:

Pasa por el punto S(-1; -2) y tiene pendiente m = -⅗.

Desarrollo

Datos:

S(-1; -2)

m = -⅗

Fórmulas:

Ecuación de la recta dado un punto y la pendiente:

y - y₁ = m·(x - x₁)

Solución

Aplicamos la fórmula dada y reemplazamos por los valores:

y - y₁ = m·(x - x₁)

y - (-2) = -⅗·[x - (-1)]

y + 2 = -⅗·(x + 1)

y + 2 = -⅗·x - ⅗

Expresamos la recta en forma explícita:

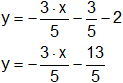
Resultado, la ecuación general de la recta es:

5·y + 3·x + 13 = 0

Graficamos:

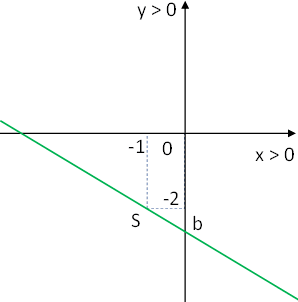
Resolvió: Ricardo Santiago Netto. Argentina

• ‹ Anterior |
• Regresar a la guía TP01
• | Siguiente ›

Ejemplo, cómo hallar y graficar rectas