Problema nº 4 de funciones lineales, distancia de un punto a una recta - TP01
Enunciado del ejercicio nº 4
Hallar la distancia del punto Q(-2; -3) a la recta de ecuación 8·x + 15·y - 24 = 0.
Desarrollo
Datos:
Q(-2; -3)
r₁: 8·x + 15·y - 24 = 0
Fórmulas:
Ecuación de la recta dado un punto y la pendiente:
y - y₁ = m·(x - x₁)
Solución
Para hallar la distancia de una recta a un punto debemos hallar una recta que pase por el punto y que sea perpendicular a la recta dada.
r₁ ⊥ r₂
Las pendientes deben ser:
La pendiente m₁ la hallamos expresando la recta r₁ en forma explícita.
r₁: 8·x + 15·y - 24 = 0
Despejamos "y":
8·x + 15·y - 24 = 0
15·y = -8·x + 24
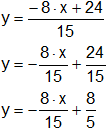
Por lo tanto:
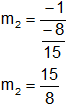
Con el valor de la pendiente m₂ y el punto dado hallamos la ecuación de r₂.
Aplicamos la fórmula dada y reemplazamos por los valores:
r₂: y - y₂ = m₂·(x - x₂)
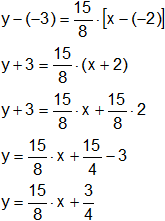
Hallamos el punto de intersección de ambas rectas por igualación:
| -8·8 - 15·15 | ·x = | 3·5 - 4·8 |
| 15·8 | 4·5 |
| -64 - 225 | ·x = | 15 - 32 |
| 120 | 20 |
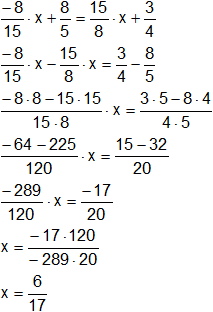
Con el valor de "x" reemplazamos en la ecuación de la recta:
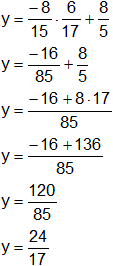
El punto de intersección de ambas rectas es:
Calculamos la distancia entre los puntos "P" y "Q" aplicando el teorema de Pitágoras:
| d² = (-2 - | 6 | )² + (-3 - | 24 | )² |
| 17 | 17 |
| d² = ( | -2·17 - 6 | )² + ( | -3·17 - 24 | )² |
| 17 | 17 |
d² = 25
d = √25
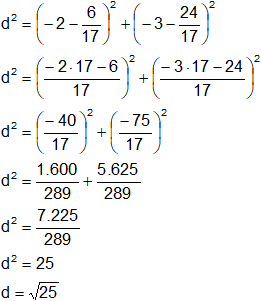
d = 5
Resultado, la distancia del punto "Q" a la recta es:
d = 5
Graficamos:
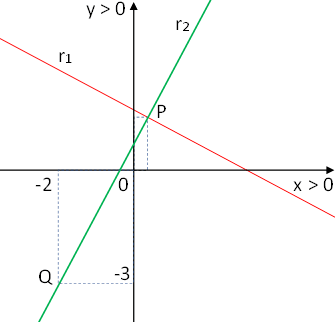
Resolvió: Ricardo Santiago Netto. Argentina
Ejemplo, cómo calcular la distancia de un punto a una recta