Problema nº 5-e de funciones lineales, operar con rectas - TP01
Enunciado del ejercicio nº 5-e
Hallar el valor del parámetro "k" de modo tal que la recta de ecuación 2·k·x - 5·y + 2·k + 3 = 0:
Sea paralela al eje "X".
Desarrollo
Datos:
r: 2·k·x - 5·y + 2·k + 3 = 0
r ∥ X
Solución
Para que se cumpla lo solicitado la pendiente debe ser nula.
m = 0
Despejamos la pendiente expresando la recta en forma explícita:
5·y = 2·k·x + 2·k + 3
| y = | 2·k·x + 2·k + 3 |
| 5 |
| y = | 2·k | ·x + | 2·k | + | 3 |
| 5 | 5 | 5 |
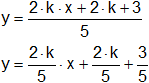
La pendiente de la recta es:
| m = | 2·k |
| 5 |
Debe cumplir:
| m = | 2·k | = 0 |
| 5 |
| 2·k | = 0 |
| 5 |
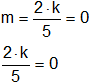
Resultado, el valor del parámetro "k" es:
k = 0
Resolvió: Ricardo Santiago Netto. Argentina
- ‹ Anterior |
- Regresar a la guía TP01
- | Siguiente ›
Ejemplo, cómo operar con rectas