Problema nº 1-m y 1-n de funciones cuadráticas, completar cuadrados - TP05
Enunciado del ejercicio nº 1-m y 1-n
Resolver las siguientes ecuaciones por el método de completar cuadrados:
m)
16·y² + 8·y - 79 = 0
Extraemos factor común el coeficiente de x²:
16·(y² + ½·y) - 79 = 0
Sumamos y restamos el cuadrado del cociente del coeficiente de x¹ por 2:
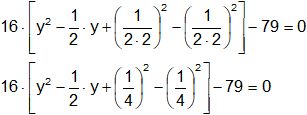
Agrupamos:
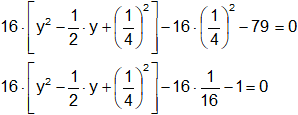
16·(y² + ½·y + ¼²) - 1 - 79 = 0
Obtenemos el trinomio cuadrado perfecto, los expresamos como cuadrado de un binomio:
16·(y² + ½·y + ¼²) - 80 = 0
• Respuesta m):
16·(y + ¼)² - 80 = 0
n)
3·z² - 2·z + 1 = 0
Extraemos factor común el coeficiente de x²:
3·(z² - 2·⅓·z) + 1 = 0
Sumamos y restamos el cuadrado del cociente del coeficiente de x¹ por 2:
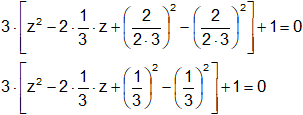
Agrupamos:
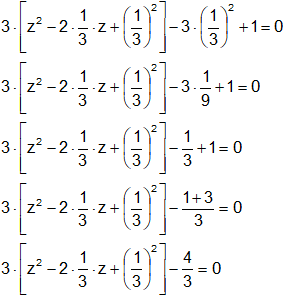
Obtenemos el trinomio cuadrado perfecto, los expresamos como cuadrado de un binomio:
• Respuesta n):
![]()
Resolvió: Ricardo Santiago Netto. Argentina
- ‹ Anterior |
- Regresar a la guía TP05
- | Siguiente ›
Ejemplo, cómo resolver ecuaciones cuadráticas completando cuadrados